Mary Lea Heger: Interstellares Natrium und Geburtstage

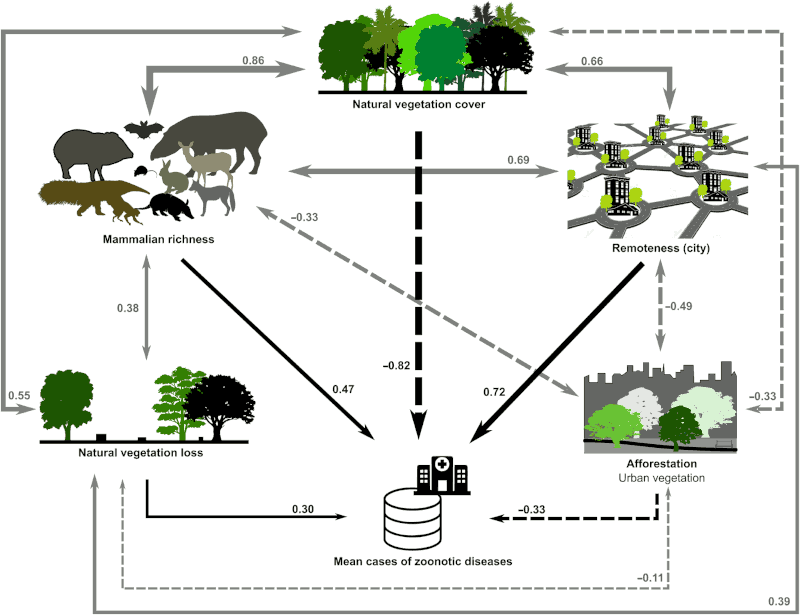
Der Stern δ Orionis in einer Aufnahme von 1927 (B5232a aus HDAP) – das war eines der zwei Objekte, in deren Spektrum Mary Lea Heger das interstellare Natrium entdeckt hat.[1]
In der DLF-Sternzeit vom 13. Juli ging es um Mary Lea Heger, die vor rund 100 Jahren entdeckte, dass es Natrium im Raum zwischen den Sternen gibt (auch wenn sie sich im verlinkten Artikel von 1919 noch nicht ganz sicher war, wo genau). Wer mal Himmelsaufnahmen aus der Zeit gesehen hat, wird ahnen, wie haarig das gewesen sein muss.
Heger hat nämlich Spektren aufgenommen, was damals überhaupt nur für sehr helle Sterne wie den oben abgebildeten δ Orionis alias Mintaka (der am weitesten rechts stehende Gürtelstern des Orion) sinnvoll ging. Aus diesen Spektren hat sie dann Radialgeschwindigkeiten abgeleitet, also im Groben beobachtete Wellenlängen von Spektrallinien bekannter Elemente mit deren auf der Erde messbaren Wellenlängen verglichen, daraus die Blau- bzw. Rotverschiebung abgeleitet und daraus wiederum bestimmt, wie schnell sich die Objekte gerade auf uns zu oder von uns weg bewegen.
Ehrlich gesagt weiß ich gar nicht, wie das damals gemacht wurde. Heute malt einem der Computer schöne Kurven und kann dann auch beliebige Funktionen dranfitten. Damals hingegen war, denke ich, schon die numerische Erfassung der Schwärzungen der Fotoplatte (bei der ihrerseits doppelte Schwärzung mitnichten doppeltes Licht bedeutet) eine echte Herausforderung. Die Wikipedia schreibt leider unter Densitometer nichts zur Geschichte dieser Geräte, und zu einer richtigen Recherche kann ich mich gerade nicht aufraffen.
Mintaka und Hegers zweites Objekt, der von uns aus kaum ordentlich zu beobachtende β Scorpii alias Akrab[2], sind beides ziemlich heiße Sterne, im Jargon Spektralklasse B mit Oberflächentemperaturen deutlich über 20000 Kelvin (die Sonne: 6000 K). Weil bei diesen Temperaturen die Atome recht schnell unterwegs sind, wenn sie Photonen absorbieren, sind die Linien solcher Sterne in der Regel breit (vgl. Dopplerverbreiterung); auf den Fotos, aus denen solche Spektren gewonnen wurden, wirken die Linien sozusagen ausgewaschen.
Tanzende und stehende Linien
Heger hat nun aber auch ein paar recht scharfe Linien von Kalzium und Natrium in den Spektren dieser Sterne gefunden, und zwar in Absorption, was heißt: Irgendwo zwischen da, wo das Licht herkommt und Hegers Spektrographen muss es Kalizum- und Natriumatome geben, die das Licht der passenden Wellenlängen absorbiert (und dann wieder woandershin emittiert) haben. Und davon nicht zu knapp.
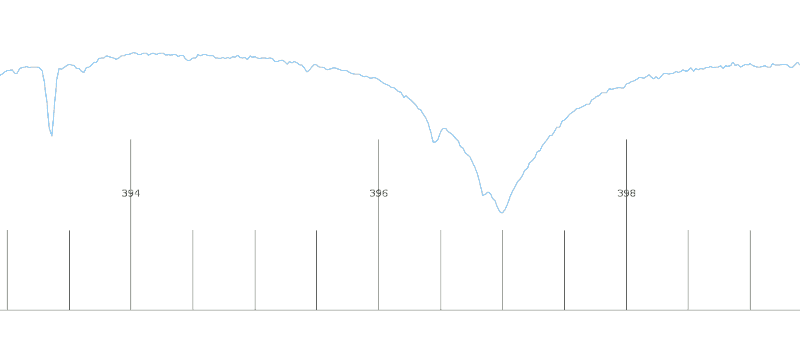
Ein modernes Spektrum von β Ori (vom FEROS-Spektrographen der ESO, HD36485_1069462_2014-08-24T08:30:43.517_S0.5x11_1x1_UVB_NOD). Auf der x-Achse ist die Wellenlänge in Nanometer, auf der y-Achse die Flussdichte in Instrumenteneinheiten. Gezeigt ist die Umgebung der Fraunhofer-Linien H (Labor: 393,368 nm) und K (Labor: 396,847 nm) des einfach ionisierten Kalziums. Links ist eine relativ schmale und unstrukturierte Linie zu sehen, wie sie Heger für die interstellare Absorption gesehen haben wird, rechts dann eine breite Linie mit vielen Komponenten von den Einzelsternen: die Höcker da drauf würden tanzen, wenn mensch einen Film machen würde. Nach etwas Überlegung habe ich beschlossen, mich nicht festzulegen, was welche Linie ist…
Sowohl Akrab als auch Mintaka sind zudem recht enge Doppelsterne[3]. So enge, dass sie mit damaligen Techniken wie ein Stern erschienen. Dass es sich um Doppelsterne handelt, war bekannt, weil in ihren Spektren (im Groben) jede Linie nicht ein Mal, sondern zwei Mal vorhanden ist, und die Teile eines Paars darüber hinaus regelmäßig umeinander tanzen. Die Erklärung: jeder Stern macht für sich eine Linie, die je nach Stellung in der Bahn anders dopplerverschoben ist als die seines Partners. Nun sind solche Sterne sehr schwer, und sie umkreisen sich auf relativ engen Bahnen (bei Mintaka: das Jahr ist im engen Paar 5.7 Tage lang), so dass die Bahngeschwindigkeiten bis hunderte Kilometer pro Sekunde betragen können[4]. Damit sind auch die Dopplerverschiebungen der Linien recht ernsthaft, und so ist die Natur der ersten dieser spektroskopischen Doppelsterne schon Ende des 19. Jahrhunderts aufgefallen.
Nur: Hegers scharfe Linien tanzen nicht. Sie bleiben stur stehen, während die Sterne umeinander rasen. Und damit ist klar, dass die absorbierenden Atome zumindest nicht zu den einzelnen Sternen gehören. Sie könnten im Prinzip aus der Erdatmosphäre kommen, denn die Natriumschicht in so um die 100 km Höhe, die heute für Laser-Leitsterne verwendet wird, ist in hinreichend empfindlichen Spektren durchaus zu sehen. Wie das mit damaligen Spektren war, weiß ich nicht, die Schicht als solche wurde aber erst 1929 entdeckt (was sich jedoch nur auf die spezifische Verteilung des Natriums beziehen mag – andererseits ist neutrales Natrium in Gegenwart von Sauerstoff nicht gerade stabil. Also: ich weiß es wirklich nicht).
Abgeleitete Kopfzahl: mit 30⋅3600 Sachen um die Sonne
Heger wird aber (auch wenn sie das im verlinkten Artikel nicht schreibt, weil die entsprechende Korrektur Teil der Standard-Datenreduktion war und ist) in ihren scharfen Linien doch eine Bewegung gesehen haben, nämlich um etwas weniger als 30 km ⁄ s. Das ist der Reflex der Bewegung der Erde um die Sonne, und der wäre in atmosphärischen Linien nicht zu sehen, da sich ja die Atmosphäre mit der Erde bewegt.
Die Geschwindigkeit der Erde bei ihrem Weg um die Sonne ist übrigens mit zwei Kopfzahlen schnell abgeschätzt: erstens dem Dauerbrenner 30 Millionen Sekunden pro Jahr (oder π⋅107 s, was tatsächlich die Art ist, in der ich mir das merke) und dann die 150 Millionen km (was ich mir als 1.5⋅1011 m merke) für den Radius der Erdbahn. Die Geschwindigkeit ist dann einfach Umfang der Erdbahn geteilt durch ein Jahr oder in überschaubareren Einheiten
Das “etwas weniger“ als diese 30 km ⁄ s kommt daher, dass die volle Amplitude dieser Bewegung nur bei Sternen in der Ekliptik, also der Abbildung der Erdbahn am Himmel, zu sehen ist. Geht mensch von dieser gedachten Linie weg, wird die Geschwindigkeitskomponente in Richtung des Sterns kleiner (nämlich mit dem Kosinus der ekliptikalen Breite), bis am ekliptikalen Pol gar kein Reflex der Erdbewegung mehr zu sehen ist[5].
Akrab nun steht in einem Tierkreiszeichen und von daher quasi per definitionem nahe an der Ekliptik. Auch der Orion (gleich südlich vom Stier) ist nicht weit von ihr entfernt – die ekliptikale Breite von Mintaka ist ungefähr 23.5 Grad. Deshalb taugt 30 km ⁄ s schon als Abschätzung für die Amplitude der Radialgeschwindigkeit der beiden Sterne aufgrund der Bewegung der Erde um die Sonne.
Mit 10⋅3600 Sachen mit der Sonne durch die Strom
Tatsächlich konnte Mary Lea Heger die Rotverschiebungen ihrer scharfen Linien und unscharfen Linien messen und kam auf folgendes Geschwindigkeiten (alles in km/s):
| Objekt | β Sco | δ Ori |
|---|---|---|
| Natrium | -9.2 | 17.6 |
| Kalzium | -8.5 | 18.7 |
| RG des Systems | -11.0 | 15.2 |
| Sonnenbewegung | -10.7 | 18.1 |
Die „Sonnenbewegung“ ist dabei das, was damals schon gemessen war als Bewegung der Sonne gegenüber der allgemeinen galaktischen Rotation von etwa 200 km ⁄ s – wie die damals darauf gekommen sind, ist eine ganz eigene Geschichte –, projiziert auf den Richtungsvektor zum jeweiligen Stern. Die „Radialgeschwindigkeit (RG) des Systems“ hingegen ist die Geschwindigkeit, mit der der Schwerpunkt der jeweiligen Sternsysteme auf uns zukommt oder sich von uns entfernt.
Dass die Sonnenbewegung und Radialgeschwindigkeiten hier recht eng beieinander liegen, ist übrigens kein Zufall. Beide Sterne sind wie gesagt heiße B-Sterne, und diese sind[6] nach astronomischen Maßstäben sehr jung, gerade erst (also: vor ein paar oder ein paar zehn Millionen Jahren) aus Gaswolken geboren. Die Gaswolken wiederum laufen sehr brav mit der allgemeinen galaktischen Rotation mit. Sie können gar nicht anders, denn anders als die Sterne kollidieren Gaswolken in Galaxien durchaus miteinander, wenn eine versucht, quer zum Strom zu schwimmen. Wenn sie dann kollidieren, verlieren sie rasch ihre Eigengeschwindigkeiten (und produzieren sehr wahrscheinlich noch eifrig Sterne). Was übrig bleibt, läuft wieder brav mit dem Rest der Galaxis.
Sterne hingegen können sich frei durch die Galaxis bewegen, weil sie praktisch nie mit anderen Sternen kollidieren – für einen Stern, kompakt wie er ist, ist die Galaxis quasi ein Vakuum, wenn auch eins mit Gavitationsfeld. Gerät ein Stern allerdings in die Nähe schwerer Dinge (wie etwa solchej Wolken), wird er ein wenig aus seiner Bahn gehoben, und das äußert sich am Ende in Eigengeschwindigkeiten wie der Sonnenbewegung von oben. Junge Sterne hatten noch keine Zeit, diese Sorte Schwung zu holen, und so ist die Radialgeschwindigkeit oben eigentlich nichts anderes als die Sonnenbewegung.
Auch wenn Heger keine Fehlerschätzungen angibt, ist die Übereinstimmung der Geschwindigkeiten der scharfen Linien und der Sonnenbewegung umwerfend gut, jedenfalls, wenn mensch die Schwierigkeiten der in diese Tabelle eingehenden Messungen bedenkt. Tatsächlich gibt die Wikipedia für die Radialgeschwindigkeit des Gesamtsystems Akrab − 1±2 km ⁄ s gegen Hegers -11; in einem System aus sechs Sternen muss das noch nicht mal auf ein Problem bei Heger hindeuten, aber ganz ehrlich: Ich wäre sehr verwundert, wenn sie besser als auf, sagen wir, 5 km/s hätte messen können.
Hegers Fazit
Entsprechend war Heger in ihren Schlussfolgerungen vorsichtig:
The agreement of the velocity obtained from the D lines …
![[RSS]](../theme/image/rss.png)