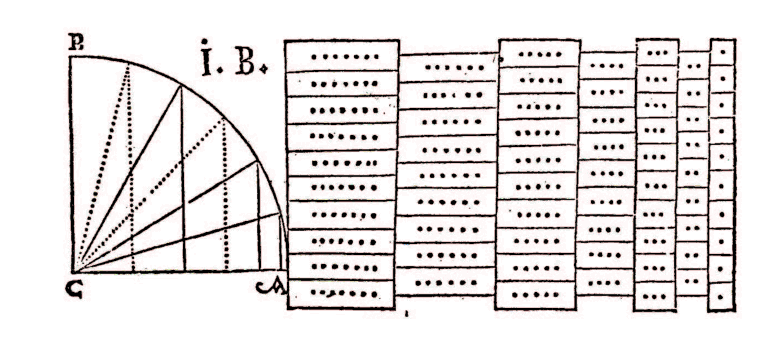
„Reimers' Diagramm“: Für 400 Jahre der einzige Hinweis darauf, wie Jost Bürgi wohl seine Sinustabelle berechnet hat. Nicht mal Kepler hat das Rätsel lösen können.
Ein Geheimnis, das im antiken Griechenland ein wenig angekratzt wurde, über das dann Gelehrte in Indien und Arabien nachgedacht haben, für das in der zweiten Hälfte des 16. Jahrhunderts ein wandernder Schweizer Uhrmacher eine genial einfache Lösung fand, von der aber die Nachwelt nur ein paar kryptische Referenzen hat, bis ein unerschrockener Wissenschaftler in den Tiefen längst vergessener Bibliotheken ein Manuskript entdeckt, das des Rätsels Lösung enthält: Es gibt Geschichten, die klingen nach einem Roman von Umberto Eco (oder, je nach Temperament und/oder Geschmack, Dan Brown) und sind doch wahr.
Auf die Geschichte von Jost Bürgis Sinusberechnung bin ich über die DLF-Sternzeit vom 27.2.2022 gekommen, und sie geht ungefähr so: Nachdem Hipparchos von Nicäa so um die 150 vdcE[1] nicht nur den ersten brauchbaren Sternkatalog vorgelegt, sondern auch die ersten ordentlichen Rezepte angegeben hatte, wie mensch für jede Menge Winkel den zugehörigen Sinus[2] ausrechnet, gab es zur Berechnung trigonometrischer Funktionen sehr lange nicht viel Neues.
Klar, der große Ptolomaios, genau, der mit dem Weltbild, hat Hipparchos' Methode zur Berechnung des Sinus über regelmäßige Vielecke kanonisiert. In Indien gab es einige Fortschritte – etwa den Übergang von der Sehne zum Sinus –, in Arabien wurden verschiedene Ergebnisse zusammengetragen und systematisiert, aber immer war es eine mühsame, geometrisch insprierte, endlose Rechnerei.
Und dann kommen wir in die frühe Neuzeit in Europa, genauer die zweite Hälfte des 16. Jahrhunderts. Kopernikus hat noch einmal ganz klassisch den Sinus mit Vielecken berechnet, während er die Konflikte zwischen Ptolomaios und der Realität untersuchte. In Italien macht sich allmählich Galileo bereit, die Physik als experimentelle Naturwissenschaft zu etablieren. Und in Kassel, beim wissenschaftsbegeisterten hessischen Landgraf Wilhelm IV, sammeln sich ein paar Mathe- und Astro-Nerds, die beim ebenso berühmten wie fiesen Tycho gelernt haben, unter ihnen Nicolaus Reimers, der das kryptische Bild über diesem Post veröffentlicht hat, vermutlich, weil er versprochen hatte, nicht mehr zu verraten.
Bürgis geniale Methode
Es weist auf ein Verfahren zur Berechnung von Werten der Sinusfunktion hin, das nichts mehr mit den umschriebenen Polygonen des Hipparchos zu tun hat. Sein Erfinder, der Toggenburger Uhrmacher-Astronom-Erfinder Jost Bürgi, hatte zu dieser Zeit ein großes Tabellenwerk vorgelegt, mit dem mensch auch ohne Taschenrechner rausbekommen konnte, wie viel wohl sin(27∘ 32’ 16’’) sei[3]. Offensichtlich funktionierte die Methode. Doch hat Bürgi – Autodidakt und vielleicht etwas verschroben – die Methode nie richtig veröffentlicht, und so brüteten MathematikerInnen, unter ihnen wie gesagt Johannes Kepler, der immerhin die Sache mit den Ellipsenbahnen im Planetensystem rausbekommen hat, lang über der eigenartigen Grafik. Und kamen und kamen nicht weiter.
Das war der Stand der Dinge bis ungefähr 2014, als der (emeritierte) Münchner Wissenschaftshistoriker Menso Folkerts im Regal IV Qu. 38ª der Universitätsbibliothek in Wrocław auf eine lange übersehene gebundene Handschrift stieß. Ein wenig konnte er ihre Geschichte nachvollziehen: Jost Bürgi persönlich hatte das Werk Kaiser Rudolf II – dem Mäzen von Tycho und Kepler – am 22. Juli 1592 (gregorianisch) in Prag übergeben, was ihm eine Zuwendung von 3000 Talern eingebracht hat. Ich habe leider nicht die Spur eines Gefühls, wie sich der Betrag mit modernen Drittmittelanträgen vergleicht. Die Form des Antrags jedenfalls ist aus heutiger Sicht als unkonventionell einzustufen.
Das Werk fand seinen Weg in das Augustinerkloster im unterschlesischen Sagan (heute Żagań). Wie es dort hinkam, ist nicht überliefert, aber mensch mag durchaus eine Verbindung sehen zu Keplers Aufenthalt in Sagan in den Jahren von 1628 bis 1630. Vielleicht hat er das Buch ja nach seinen Diensten in Prag mitgenommen, auf seinen verschiedenen Wanderungen mitgenommen und schließlich selbst im Kloster gelassen? Aber warum hätte er dann über Bürgis Methode gerätselt?
Wie auch immer: Im Gefolge des Reichsdeputationshauptschlusses wurde das Kloster 1810 aufgelöst – ich stelle mir das ein wenig vor wie in Poes „Die Grube und das Pendel“ –, und der Bestand der Bibliothek fiel an die Universität Breslau, die wiederum nach dem zweiten Weltkrieg zur polnischen Uni Wrocław wurde.
In diesem geschichtsträchtigen Manuskript erklärt Bürgi seinen Algorithmus. Dargestellt ist das in der Abhandlung von Folkerts et al (arXiv:1510.03180), in der sich auf den Seiten 11 und 12 auch die Auflösung für Reimers' Rätsel findet. Etwas schöner beschreibt das Verfahren Denis Roegel in seinem Aufsatz Jost Bürgi's skillful computation of sines. Dort wird auch Bürgis mutmaßliche Grundeinsicht besser erläutert, nach der der Sinus einfach das Ding ist, das, modern gesprochen, nach zweifacher Ableitung sich selbst (mal minus eins) ergibt. Das ist der mathematische Hintergrund dafür, dass folgendes Stück Python tatsächlich relativ schnell zu einer Tabelle der Sinuswerte von n im ersten Quadranten gleichverteilten Winkeln konvergiert:
tot_sines = list(range(n+1))
for iter_index in range(n_iter):
intermediates = [tot_sines[-1]//2]
for tot in reversed(tot_sines[1:-1]):
intermediates.append(intermediates[-1]+tot)
tot_sines = [0]
for diff in reversed(intermediates):
tot_sines.append(tot_sines[-1]+diff)
return dict((k*math.pi/2/n, v/tot_sines[-1])
for k, v in enumerate(tot_sines))
– es ist, glaube ich, unmöglich, zu verstehen, was hier passiert (und warum), ohne den Roegel oder zumindest den Folkerts gelesen zu haben. Aber ich könnte andächtig werden angesichts so simpler Manipulationen, die so schnell zu richtig vielen Stellen einer transzendenten Funktion wie des Sinus führen.
Ein numerischer Traum
Wie schnell das mit den vielen Stellen bei Bürgis Algorithmus geht, zeigt folgende Grafik:
Hier läuft horizontal der Winkel – und der Algorithmus funktioniert wirklich nur, wenn das einen rechten Winkel einschließt –, vertikal die Iterationen von Bürgis Algorithmus. Die Farben entsprechen dem dekadischen Logarithmus der Abweichung der Bürgi-Ergebnisse von dem, was die Python-Standardbibliothek gibt, im Groben also die Zahl der Stellen, die der Algorithmus richtig hinbekommt. Mehr als 18 geht da schon mal nicht, weil die Zahlen von Python in 64-bittigen IEEE-Fließkommazahlen („double precision“) kommen, und mehr als 18 Dezimalstellen sind da nicht drin (in der Grafik steckt die Zusatzannahme, dass wir von Zahlen in der Größenordnung von eins sprechen).
Mithin gewinnt der Algorithmus pro Iteration ungefähr eine Dezimalstelle, und das gleichmäßig über den ganzen Quadranten. DemoprogrammiererInnen: billiger kommt ihr, glaube ich, nicht an eine beliebig präzise Sinustabelle ran.
Spannend fand ich noch die kleinen dunkelblauen Klötzchen ganz unten in der Grafik: Hier werden sich Bürgi und Python offenbar auf Dauer nicht einig. So, wie ich das geschrieben habe, würde ich fast eher Bürgi vertrauen, denn bei den Ganzzahlen, die da verwendet werden, kann eigentlich nichts schief gehen. Andererseits sind Fließkommazahlen eine heikle Angelegenheit, insbesondere, wenn es ums letzte Bit geht. Um mich zu überzeugen, dass es nur um genau jenes unheimliche letzte Bit geht, habe ich mir geschwind eine Funktion geschrieben, die die Fließkommazahlen vinär ausgibt, und der Code gefällt mir so gut, dass ich sie hier kurz zeigen will:
import struct
_BYTE_LUT = dict((v, "{:08b}".format(v)) for v in range(256))
def float_to_bits(val):
return "".join(_BYTE_LUT[v] for v in struct.pack(">d", val))
Mit anderen Worten lasse ich mir geschwind ausrechnen, wie jedes Byte in binär aussehen soll (_BYTE_LUT), wobei die Python-Bibliothek mit dem 08b-Format die eigentliche Arbeit macht, und dann lasse ich mir die Bytes der Fließkommazahl vom struct-Modul ausrechnen. Der einzige Trick ist, dass ich das Big-end-first bestellen muss, also mit dem signfikantesten Byte am „linken“ Ende. Tue ich das nicht, ist z.B. auf Intel-Geräten alles durcheinander, weil die Bits in der konventionellen Schreibweise daherkommen, die Bytes aber (wie bei Intel üblich) umgedreht, was ein furchtbares Durcheinander gibt.
Jedenfalls: Tatsächlich unterscheiden sich die Werte schon nach 20 Iterationen nur noch im letzten bit, was für 45 Grad alias π/4 z.B. so aussieht:
45 0011111111100110101000001001111001100110011111110011101111001101 0011111111100110101000001001111001100110011111110011101111001100
Ich lege mich jetzt mal nicht fest, was das „bessere“ Ergebnis ist; ich hatte kurz überlegt, ob ich z.B. mit gmpy2 einfach noch ein paar Stellen mehr ausrechnen sollte und sehen, welches Ergebnis näher dran ist, aber dann hat mich meine abergläubische Scheu vor dem letzten Bit von Fließkommazahlen davon abgehalten.
Wer selbst spielen will: Meine Implementation des Bürgi-Algorithmus, der Code zur Erzeugung der Grafik und die Bitvergleicherei sind alle enthalten in buergi.py.
| [1] | Das vdcE bringe ich hiermit als Übertragung von BCE, before the Christian era, in Gebrauch. Und zwar, weil v.Chr völlig albern ist (es ist ja nicht mal klar, ob es irgendeine konkrete Figur „Christus“ eigentlich gab; wenn, ist sie jedenfalls ganz sicher nicht zur aktuellen Epoche – also dem 1. Januar 1 – geboren) und „vor unserer Zeitrechnung“ ist auch Quatsch, denn natürlich geht Zeitrechnung (wenn auch mangels Jahr 0 etwas mühsam) auch vor der Epoche. „Vor der christlichen Epoche“ hingegen bringt ganz schön auf den Punkt, was das ist, denn die „Epoche“ ist in der Zeitrechnung einfach deren Nullpunkt (oder halt, vergurkt wie das alles ist, hier der Einspunkt). |
| [2] | Na ja, in Wirklichkeit hat er mit der Länge der Sehne gerechnet, die ein Winkel in einem Kreis aufspannt, aber das ist im Wesentlichen das Gleiche wie der Sinus, der ja gerade der Hälfte dieser Sehne entspricht. |
| [3] | Ich bleibe natürlich bei meiner Verurteilung sexagesimaler Darstellungen aus Fußnote 1 in Wasch mir den Pelz. Das ist hier nur, weil Bürgi unglaublicherweise seinen Kram selbst sexagesimal gerechnet hat. |
Zitiert in: Mach mit bei DIT Das Verschwinden der Nacht in der Skulpturensammlung Mehrfach reflexiv: Das Linden-Museum in Stuttgart Gallische Dörfer, römische Klappmesser: Das Landesmuseum in Bonn Seuchen, Christen und das Ende des Imperiums Der Markov-Preis für die ungewöhnlichste Wortfolge
![[RSS]](./theme/image/rss.png)