Mit meinem zyTemp-Kohlendioxid-Messgerät – das, für das ich neulich Software gebastelt habe – bin ich natürlich gleich in die Welt gezogen, um mal zu sehen, wo es überall CO2 (und mithin plausiblerweise Corona-Aerosol) geben wird.
Der Wind und die Seuche
Nachdem mich ja zunächst sehr überrascht hat, wie deutlich sich die Anwesenheit von Menschen in rasch steigendem CO2-Gehalt der Luft in Innenräumen niederschlägt, war meine zweite große Überraschung, dass sich umgekehrt im Freien nichts tut. Also, richtig gar nichts. Selbst Autos, die mindestens eine Größenordnungen mehr CO2 emittieren als Menschen (vgl. unten), fallen schon aus ein paar Metern Entfernung im Wesentlichen nicht mehr auf. Ich musste mich schon an Kreuzungen neben die Ampeln stellen, um überhaupt ein schwaches Signal zu bekommen. Und das war kaum mehr als ein leichtes Oszillieren um ein paar ppm, während die wartenden Autos vor sich hinstanken und dann losbrausten. So sehr es nach Abgasen stank – CO2 ist im Nahbereich von Autos kein Problem.
Die gute Nachricht ist also: Wenn CO2 ein guter Indikator ist, wie schlimm es mit Aerosol sein kann – real verschwindet Aerosol im Regelfall aus hinreichend ruhiger Luft durch Niederschlag, was CO2 nicht tut – ist praktisch sicher, dass an der frischen Luft bei nicht völlig irren Wetterlagen SARS-2 allenfalls durch Tröpfchen übertragen wird.
Umgekehrt war meine Sorge ja immer der öffentliche Verkehr, und so habe ich mit Hingabe in verschiedenen Zügen gemessen. Als Referenz: Frischluft liegt derzeit hier irgendwo zwischen 280 und 350 ppm CO2. In einem halb vollen ICE habe ich zwischen 800 und 1400 ppm gemessen (interessanterweise nicht so ganz korreliert mit den Bahnhofsstopps; die Bahn kennend, vermute ich eine Nicht-so-ganz-wie-gedacht-Funktion der Lüftung in dem Wagen, in dem ich saß). Ein vollbesetzter IC-Zug der SBB war zwischen 800 und 1050 dabei, ein leerer Nahverkehrszug bei etwa 400, ein halb voller eher bei 700.
Bei solchen Dynamiken ist wohl klar, dass hinreichend viel frisches Aerosol in der Luft sein wird, jedenfalls, solange nicht alle Passagiere mit richtig sitzenden FFP2-Masken dahocken, und sowas habe ich noch nicht mal dort gesehen, wo es wie in Berlin und Bayern gesetzlich gefordert ist oder war. Es muss also im letzten Winter weit mehr Ansteckungen in Zügen gegeben haben als das RKI in seinen Ausbruchshistogrammen (z.B. S. 12 am 9.3.2021) mit den kleinen roten Säulen andeutet. Aber ok, sie haben ja immer dazugesagt, „Clustersituationen in anonymen Menschengruppen (z.B. ÖPNV, Kino, Theater)“ seien fast sicher unterrepräsentiert.
Atmende Blumen
Aber ich hatte auch anderweitig viel Spaß mit dem Gerät. So war ich neulich verreist, und in der Wohnung verlief die CO2-Konzentration so:
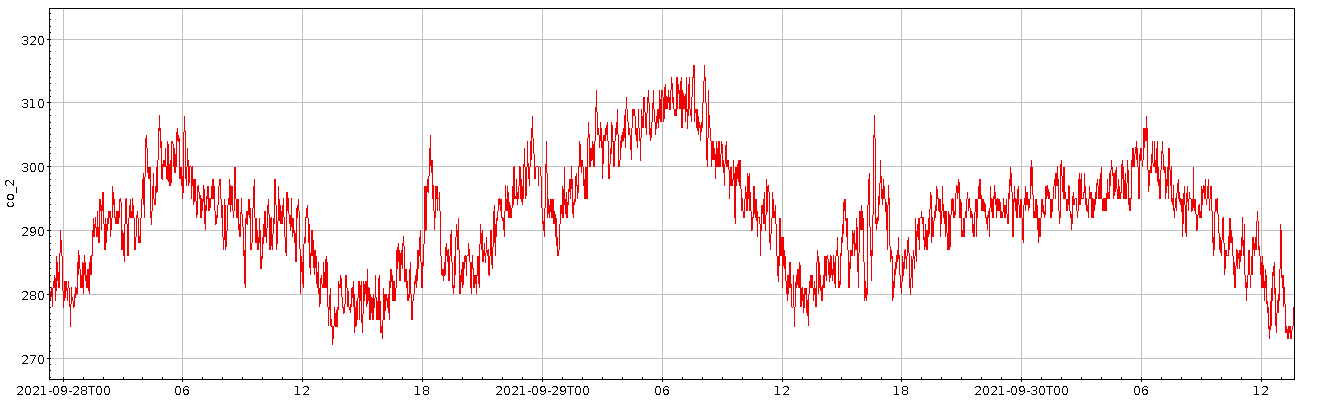
CO2-Konzentrationen in meinem Wohnzimmer während der Abwesenheit aller BewohnerInnen. Zeiten sind in UTC.
Wohlgemerkt: Da war niemand. Es könnte sein, dass sich hier einfach Schwankungen in der Außenluft reflektieren; aber ich glaube zunächst mal, dass wir hier einer Birkenfeige beim Stoffwechsel zusehen; 6 Uhr UTC, wenn die Kurve sich nach unten wendet, entspricht 8 Uhr Lokalzeit und damit wohl der Zeit, in der es in dem Zimmer hell genug für Photosynthese werden dürfte; der große Peak rund um 18 Uhr am 28.9. wäre schön konsistent damit, dass die Pflanze sich zur Ruhe setzt und dazu kurz mal ihre Mitochondrien anwirft; der folgende Abfall wäre dann wieder ein Mischungseffekt, denn der Sensor lag (mehr zufällig) praktisch in den Zweigen des Ficus. Warum er, das angenommen, den Peak am 29.9. doch deutlich früher gemacht hat? Nun, vielleicht war ja Mistwetter? Oder vielleicht ist das auch alles ganz anders: das bräuchte definitiv mehr Forschung.
Rauchmelder diagnostizieren Blasenschwäche
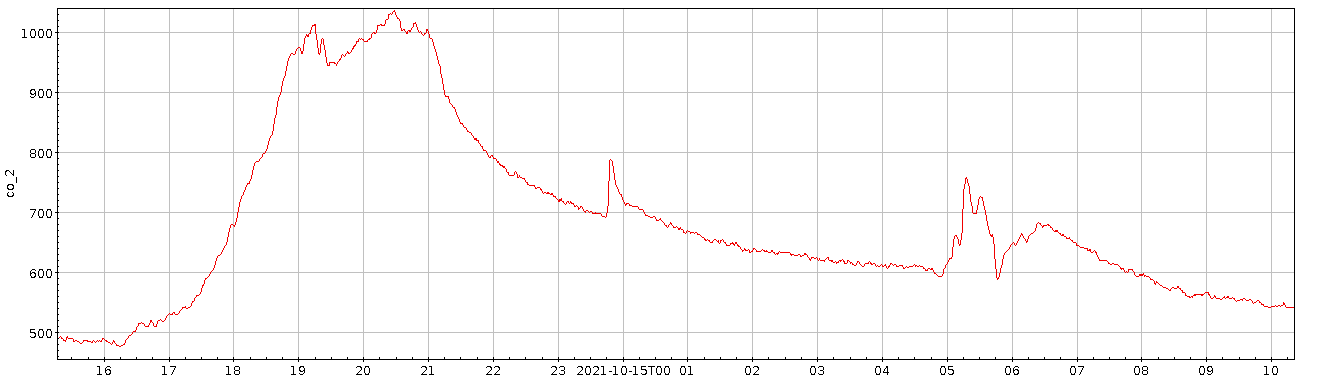
CO2-Konzentrationen in meiner Diele. Zeiten sind in UTC.
Wenig überraschend zeigt sich, dass die CO2-Konzentrationen dramatisch personenbezogene Daten sind. Der zweite Graph illustriert das an einem relativ harmlosen Beispiel: Der Sensor steht jetzt in der Diele, vor meiner Zimmertür. Deutlich zu sehen ist, dass ich an dem Tag gegen 23 Uhr geschlafen habe, oder jedenfalls, dass meine Schlafzimmertür dann zu war. Und dann bin ich kurz vor zwei mal wach gewesen, weil ich am Abend etwas viel Tee getrunken hatte. am Morgen aufgestanden bin ich um sieben, kurz vor acht habe ich mal gelüftet, und um halb neun bin ich gegangen.
Wer da etwas länger auf diese Weise zuschaut, findet viel über die BewohnerInnen von Wohungen heraus – angefangen davon, wann wie viele Menschen wo in der Wohnung sind –, und das im Zweifelsfall auch automatisiert unter vielen Menschen. Ich habe dabei lediglich zwei Messwerte pro Minute genommen. Das ginge, so würde ich schätzen, für eine ganze Weile mit den zumindest hier im Haus recht verbreiteten per Funk auslesbaren Rauchmeldern ganz gut, ohne dass ihre Batterien gleich alle wären – für die Betreiber und, weil die Krypto von den Teilen schon aus Stromspargründen sehr wahrscheinlich lausig ist, vermutlich auch ungefähr für jedeN, der/die sich hinreichend intensiv für das Leben der Anderen interessiert.
Nachdenken nur für 50W?
Schließlich bin ich jeden Tag wieder aufs Neue fasziniert, wie schnell ich in meinem Büro schlechte Luft verbreite.
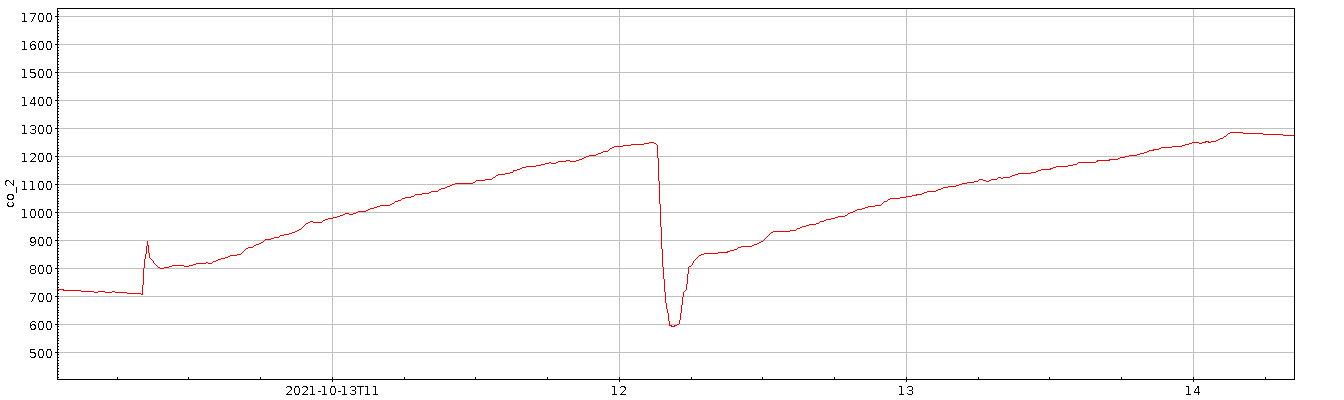
CO2-Konzentrationen in meinem Büro; ich komme von der Mittagspause zurück, arbeite, und lüfte ein Mal. Zeiten sind in UTC.
An dieser Kurve ist viel zu sehen, unter anderem, dass sich offenbar die Luft in dem Raum doch recht schnell mischt; das würde jedenfalls schön erklären, warum es beim Lüften kurz nach 12 Uhr UTC so eine Delle nach unten gibt: Das ist die Frischluft von außen, die ziemlich direkt an den Sensor weht, sich dann aber innerhalb von fünf Minuten mit meinen im Raum gebliebenen Abgasen mischt.
Diese schnelle Homogenisierung ist wesentlich für eine Überlegung, die sich für mich da aufdrängt: Wie viel CO2 mache ich eigentlich? Das geht so:
In den 96 Minuten von 10:30 bis 12:06 habe ich die Konzentration von 808 auf 1245 ppm erhöht, was einer Rate von
entspricht[1] (ich habe das nicht aus dem PNG, sondern noch im Plotprogramm selbst abgelesen). Ein zweiter Datenpunkt ist nach Lüften und Mischen: Da ging es von 12:17 bis 14:08 von 837 auf 1288 ppm, was auf eine Rate von 0.068 ppm/s führt.
Aus den beiden Werten würde ich grob schätzen, dass ich die CO2-Konzentration in meinem Büro so etwa mit 0.07 ppm/s erhöhe, wenn ich normal arbeite; ich nenne diese Rate hier kurz δ. Unter der sicher falschen, aber vielleicht noch hinnehmbaren Annahme, dass kein CO2 entweicht und der nach den Beobachtungen plausiblen Annahme voller Durchmischung im Raum kann ich nun abschätzen, was mein Stoffwechsel so tut.
Was es dazu braucht, ist das Wissen, dass bei einem idealen Gas (was die Luft nicht ist, aber für die Abschätzung reicht es) bei „Normalbedingungen“ (die bei mir im Zimmer glücklicherweise auch nicht ganz perfekt realisiert sind) ein Mol 22.4 Liter Volumen einnimmt[2]. Unter Kopfzahl-Aspekten kann ich nicht genau sagen, warum ich mir da drei Stellen gemerkt habe. In Wirklichkeit sind 20 l/mol natürlich genau genug als Kopfzahl. Ich nenne das unten Vm.
Das ist eine Aussage über die Zahl der Gasmoleküle in einem Volumen V, denn ein Mol sind ungefähr 6e23 (so schreibe ich wieder kurz für 6⋅1023) Teilchen („Avogadro-Konstante“; außerhalb von Kopfzahlen ist die inzwischen exakt festgelegt und definiert das Mol). Mein Büro ist so in etwa fünf Meter lang, 2.5 Meter breit und drei Meter hoch, hat also V = 40 Kubikmeter Rauminhalt. Das heißt, dass sich darin
befinden. Das sind gegen 1e27 oder 1000000000000000000000000000[3] Moleküle. Diese Zahl hat einen Namen: das ist eine Quadrillarde. Aber klar: der Name ist selbstverständlich Quatsch. Ich musste ihn selbst nachsehen. Der wissenschaftliche Fachbegriff für solche Zahlen ist Gazillion. Für alle davon. Weshalb wir eben immer zehn hoch siebenundzwanzig sagen, was viel nützlicher ist.
Und dann brauche ich noch die Energie (oder hier genauer die Enthalpie, normalerweise geschrieben als ΔH) die bei der Bildung eines Moleküls CO2 auch C und O₂ frei wird; konventionell geben die Leute das nicht für ein Molekül, sondern für ein ganzes Mol (ihr erinnert euch: ganz platt 6e23 Moleküle statt nur eins) an, und die Wikipedia verrät, dass das 394 kJ/mol sind.
Jetzt baue ich das zusammen, nämlich die Erzeugungsrate von CO2 in physikalischen Einheiten (statt in ppm/s), δ⋅V ⁄ Vm, auf der einen Seite, und mein ΔH auf der anderen Seite. Es ergibt sich für meine Leistung:
Wenn mensch da die Einheiten glattzieht und bedenkt, dass ppm/s eigentlich 1e-6/s ist, muss mensch was rechnen wie:
(ich schreibe das so ausführlich, weil ich mich beim schnellen Hinschreiben prompt verrechnet habe), was rund 50 J/s (also 50 W) ergibt.
Ich habe von irgendwoher im Kopf, dass ein durchschnittlicher Mensch thermisch was wie 200 W rauspumpt, wozu dann in der Situation noch mein intensives Denken (mindestens ein halbes Kilowatt, klar!) käme. Ein schneller Blick auf duckduckgo liefert z.B. diese Seite, die eher von 100 W spricht. Immerhin: die Größenordnung ist mal wieder rausgekommen, und weil bestimmt ordentlich CO2 zu Fenster und Tür rausgeht oder vom mein Büro teilenden Papyrus zu Blättern gemacht wird, ist nicht unplausibel, dass ich ein wenig zu tief liege.
Allerdings hätte ich schon lieber etwas mehr rausbekommen, denn was im Körper stattfindet, ist ja eben nicht das C + O₂ → CO2, für das wir unsere 400 kJ/mol haben. Stattdessen finden fantastisch komplizierte Reaktionen rund um meine Mitochondrien statt, die jedenfalls noch den Kohlenstoff aus Zuckern und Fetten rauspulen müssen, so dass insgesamt deutlich weniger Energie pro Molekül freigesetzt werden wird.
Ein wenig verwandt damit ist die Frage, wie viel „Nutzenergie“ ich da wohl umsetze, also nach Abrechnen von Abwärme (was immer das bei einem wechselwarmen Wesen wie mir – nein, ich bin kein Echsenmensch – bedeuten mag). Der Lodish et al sagt, dass bei der Verstoffwechselung von Kohlenwasserstoffen und Sauerstoff in eukaryotischen Zellen für je sechs CO2-Moleküle rund 30 Moleküle ATP frei werden. Das ATP wird dann für allerlei nützliche Dinge im Körper verwendet (z.B. mein Nachdenken), geht also in erster Näherung als Nutzenergie durch. Dabei liefert ein Mol ATP 7.3 kcal, wenn es wieder zu ADP wird.
Echt. Bei den BiochemikerInnen ist immer noch alles kcal. Oder war es, als meine Ausgabe vom Lodish in ein PDF gegossen wurde; da die Kalorie seit 1948 Geschichte sein sollte, ist der Unterschied dieses Zeitpunkts zu „jetzt“ vernachlässigbar.
Aber freundlicherweise ist in der Wandlung von Kalorien in vernünftige Einheiten auch eine Kopfzahl drin, nämlich wie viel Energie es etwa braucht, um ein Gramm Wasser um ein Kelvin (oder Grad) zu erwärmen. Das sind 4.2 J, und das ist, modulo für Abschätzungen irrelevanter Details, eine Kalorie. Mithin ist die Reaktionsenthalpie (also grob, wie viel Energie freiwird) der ATP-ADP-Reaktion in vernünftigen Einheiten 31 kJ/mol.
Wenn ich jetzt zurückgehe zu meiner CO2-Erzeugungsrate von δ⋅V ⁄ Vm = 0.1⋅10 − 3 mol/s, komme ich auf:
Ok, das wird wieder eine kräftige Unterschätzung sein. Aber selbst wenn da ein Faktor vier drin wäre: Ich finde, dass ich total energiesparend funktioniere.
Demnächst: Was passiert mit meinem CO2-Umsatz, wenn turne oder schlafe?
| [1] | Hier war mal eine Fußnote, die mich sehr kompromittiert hat, die jetzt aber nicht mehr so sehr zutrifft. Zwecks Transparenz und Selbstkasteiung ist er in einem Blog-Post zu Mathe mit RST dokumentiert. |
| [2] | Wie das auszurechnen ist, verrät die Wikipedia. |
| [3] | Ah, bei solchen Zwecken glänzt mein Lieblingseditor vi: Getippt habe ich das als 1<ESC>27i0<ESC>. Ha! |
Zitiert in: Kohlenstoff-Stoffwechsel des Menschen: Nur über Bande schlimm Menschliche Leistung: Hundertfünfzig Watt Kohlendioxid auf dem Balkon Math with ReStructuredText and Pelican
![[RSS]](./theme/image/rss.png)