Tag Wissenschaft

  • Wenig Neues unter der Sonne

    12021:121:7 ( 2021-05-02)
    Eine Hebamme bringt ein Neugeborenes mit Hörnern

    Fantasien zu Impfwirkungen aus dem frühen 19. Jahrhundert (Quelle).

    Im immer wieder großartigen Public Domain Review – den ich schon deshalb mag, weil fast alles ohne Javascript geht – war neulich ein Essay über das Georgian Britain’s Anti-Vaxxer Movement von Erica Eisen; es geht um frühe ImpfskeptikerInnen, und ich fand schon bemerkenswert, wie sehr sich die Motive damalis und der heute ähneln.

    Teils ist das ganz verständlich, weil etwa die Funktionsweisen von Religion historisch ziemlich konstant sind. Insofern wundert die Konstanz des Arguments über Impfen als Interferenz mit Gottes Plan nicht:

    The Small Pox is a visitation from God, but the Cow Pox is produced by presumptuous man: the former was what heaven ordained, the latter is, perhaps, a daring violation of our holy religion.

    —William Rowley, Cow-Pox Inoculation: No Security Against Small-Pox Infection (London: J. Barfield, 1805), 11.

    Umgekehrt ist erschütternd, dass die (zumindest im Fall von SARS-2) offensichtliche Abwägung zwischen möglichem Schaden und manifestem Nutzen häufig immer noch so auszugehen scheint wie unter Verhältnissen, die Eisen so beschreibt und in denen das tatsächlich ganz anders hätte sein können:

    These concerns were not allayed by the poor sanitation and medical standards that sometimes characterized the public vaccination hospitals created to serve Britain’s urban poor: at such places, the vaccines made available to patients often came not directly from cows but from the pustules of vaccinated children in the area, who may or may not have received a thorough medical check before being lanced for their “donation”. As a result, parents were not wholly unjustified in their fears that an injection meant to ward off one deadly disease might simply lead to their child being infected with another one.

    Keine Überraschung ist dabei natürlich die Beständigkeit von Armut als größtem Risikofaktor; zur der modernen Form berichtete neulich der Deutschlandfunk:

    Wo Menschen in beengten Wohnverhältnissen lebten, sei die Gefahr sich anzustecken größer als im großzügig angelegten Einfamilienhaus, sagte er in einer Landtagsdebatte in Düsseldorf. Der CDU-Chef und Unions-Kanzlerkandidat verwies dabei auf das Beispiel Köln, wo im Stadtteil Chorweiler die Inzidenz bei 500 und in Hahnwald dagegen bei 0 liege.

    Aber die wirklich beeindruckenden Parallelen liegen in völlig abseitigen Fantasien über mögliche Impfwirkungen und die Motivationen dahinter: Die gehörnten Neugeborenen aus dem Eingangsbild treffen sich da gut mit den Chips von Bill Gates, und die Angriffe aufs klare Denken gehen auch ganz regelmäßig über imaginierte Bedrohngen von Kindern, etwa im Eingangsbild oder wenn pockennarbige Monstren sie in kleine Minotauren verwandeln

    Insofern: Ein wirklich lohnender Artikel mit, wie üblich beim PDR, vielen schönen Bildern.

  • 35 Jahre Tschernobyl

    12021:116:1 ( 2021-04-26)
    Sonne hinter Kühlturm

    Noch ein Grund, warum kleine AKWs stinken: Nicht mal klasse Kühltürme (wie den hier in Biblis) gibts mehr.

    Unter den deutschsprachigen Fortune Cookies von Debian sind jede Menge Witze des Typs „Wenn Microsoft Autos bauen würde… müssten wir alle auf Microsoft-Benzin™ umsteigen“ oder ”…würden die Warnlämpchen für Öl, Batterie, Benzin, und Motorschaden durch ein einziges »Genereller Auto-Fehler«-Lämpchen ersetzt.“

    Da wirkt es schon etwas befremdlich, wenn ausgerechnet Bill Gates jetzt Atomkraftwerke bauen will, und zwar jede Menge davon. Sein Laden Terrapower [Vorsicht: CPU-intensive Webseite] versucht, mit dem üblichen Marketing-Dummschwätz („Best-in-class talent“ – wer denkt sich sowas aus? Und meint, auch nur irgendwer würde da nicht nur die Augen verdrehen?) Schmelzsalzreaktoren wieder aus der Kiste klar schlechter Ideen rauszuziehen.

    Wer sich das bei Terrapower verlinkte Interview mit Gates [Vorsicht: Link zu youtube] ansieht, versteht vielleicht, weshalb er da alle Vernunft fahren lässt: Er hat genug Herz, dass ihm die Nöte der ärmeren Hälfte der Welt nicht ganz gleich sind, aber er glaubt zu sehr an Markt und Kapitalismus, um einzusehen, dass es diesen Leuten nicht wegen mangelnder Produktion dreckig geht, sondern wegen Markt, Eigentum und Ungleichheit, gerade auch im Zugriff auf Bildung und Produktionsmittel (sagen wir: der Boden, der entweder unsere Schweine oder ihre Bäuche füttert). Und so kommt er auf den Trichter, dass billigere Energie doch bestimmt den Kapitalismus auf eine weniger menschenfresserische Route bringen müsste.

    Obwohl ich Gates also durchaus halbwegs guten Willen unterstelle, kommt er doch wieder nur mit dem Unsinn, mit dem die Bombenbauer schon in den 50ern versuchten, ihren Atomstaat zu verkaufen (damals heiß das „electricity too cheap to meter“[1]):

    This is just like a candle. Our flame is taking the normal, depleted Uranium, the 99.3% that's cheap as heck and there's a pile of it sitting in [Paducah?], Kentucky that is enough to power the United States for hundreds and hundreds of years. You're taking that and you're converting it to [leicht verschämt] Plutonium, and you're burning that, and we have super-high power densities, we have, you know, total fail... fail-safe. Any reactor that a human has to do something... that's a little scary. [Audio]

    „Total fail-safe“ vom Microsoft-Vordenker und Vater des legendären Webservers IIS hat natürlich nochmal einen besonderen Geschmack, etwa angesichts der Exchange-Katastrophe, von der ich neulich am Rande gestreift wurde. Und dann sollen die Menschen draußen bleiben und... nun, wen genau die nötige Wartung machen lassen? Microsofts Roboter? Und das alles in den Ländern, in denen die vier Milliarden Ärmsten wohnen?

    Das ist so offensichtlich absurd, dass ich mich frage, warum Gates es überhaupt sagt.

    Nur ist das nicht das Thema.

    Wer über Atomkraft nachdenkt, sollte zumächst beim prinzipiellen Alptraum jeder Sorte Technik anfangen: Eine Kettenreaktion ist zunächst immer höchst instabil, denn ein Neutron muss dabei immer ganz genau ein weiteres Neutron erzeugen. Ist es auch nur ein Hauch weniger, geht der Reaktor exponentiell aus. Ist es ein Hauch mehr, geht der Reaktor exponentiell durch. Das ist, ganz prinzipiell, nichts, womit mensch basteln möchte, und das Gegenprinzip zu Gates' „fail safe“.

    Dass herkömmliche (langsame Uran-) Reaktoren überhaupt beherrschbar sind, liegt an einer Laune der Natur, nämlich einer sehr schmalen Neutronen-Absorptionslinie des Uran-238 gerade im Bereich von „thermischen” Neutronen (also welchen mit ein paar hundertstel eV). Nimmt nämlich die Reaktionsrate eines solchen Reaktors zu, wird er heißer, die Linie verbreitert sich thermisch, es kommt zu mehr Absorption von Spaltneutronen, die Reaktionsrate nimmt ab. Nimmt dagegen die Reaktionsrate ab, wird die Linie thermisch schmaler, die Absorption nimmt ab, die Reaktionsrate steigt wieder ein wenig.

    Das ist der wesentliche Grund, warum Brennstäbe ausgewechselt werden lange bevor alles U-235 gespalten ist und weshalb die Wiederaufbereitung schon vor der Zulassung von Mischoxid-Brennelementen (die Plutoium enthalten) nicht völlig unplausibel schien: Irgendwann muss mensch wieder U-238 in die Brennstäbe bringen, um die Regelung zu halten. Das heißt auch: Ein solcher Reaktor wird immer instabiler, je länger er ungewartet läuft. Zu den großen Wundern dieser Welt gehört, dass nicht ständig vernachlässigte Reaktoren durchgehen.

    Nun lassen sich ähnliche lokale Stabilitätspunkte auch künstlich herstellen („negativer Temperaturkoeffizient“), und die Wikipedia erklärt ganz gut, wie sich die Schmelzsalz-Fans das so vorstellen. Aber selbst wenn mensch ihnen diese Ideen abnimmt, sind das in all diesen Fällen nur kleine Dellen an einem langen, exponentiellen Hang einer sich entweder selbst-rückgekoppelt abschwächenden (Puh!) oder verstärkenden Reaktionsrate. Sowas will mensch als technisches Design ganz grundsätzlich nicht, wenns irgendwie anders geht.

    Und natürlich geht es anders, solange lediglich hinreichend Strom in vernünftigem Umfang (also: wenn wir uns komplett sinnlose Stromverschwendung wie die der terrapower-Webseite oder oder offensiv schädliche Stromverschwendung wie Elektroautos sparen) das Ziel ist. Wer sich die Mühe macht, die historischen Kernkraft-Programme in aller Welt anzusehen, wird feststellen, dass immer staatliches Geld und am Schluss das Interesse dahinterstand, die Technologie für die Bombe wenigstens in der Hinterhand zu haben. Plus vielleicht noch die Fantasie, einer politischen Einflussnahme im Stil der OPEC-Aktion nach dem Jom Kippur-Krieg länger widerstehen zu können – nicht ganz zufällig fing der ganz große Geldstrom in die „zivile“ Nutzung der Kernspaltung erst nach 1973 so richtig an. Weder Kosten (die immer exorbitant waren) noch Energieproduktion als solche waren je ein ernstzunehmendes Argument bei Atomprogrammen.

    Dementsprechend könnte mensch Gates' Gerede mit einem Achselzucken vergessen, wenn er mit seinem (natürlich absurden) „helft den Armen“-Narrativ nicht gerade den Staaten im globalen Süden eine Erzählung liefern würde, warum sie auch Bombentechnologie haben sollten. Denn natürlich ist Quatsch, dass bei Schmelzsalzreaktoren keine Proliferationsgefahr bestehe; wer Neutronen im Überfluss hat, kann mit etwas Chemie und vielleicht einer Handvoll Zentrifugen auch Bomben bauen. Punkt.

    Gates selbst räumt das – diskurv geradezu suizidal – ein: „super-high power densities“. Hohe Energie- und damit auch Neutronendichten sind das stärkste Argument gegen diese Sorte von Technik. Wer einen Eindruck von der Rolle von Energiedichte bekommen will (und sich um Umweltsauerei nicht kümmert), kann mal eine vollgeladene NiMH-Zelle (noch besser wäre NiCd, aber das will mensch dann wirklich nicht in die Umwelt pesten) und eine vollgeladene Lithium-Ionen-Zelle in ein Feuer werfen. Eins macht bunte Farben, das andere ein verheerendes Feuerwerk [nur zur Sicherheit: Nein, Feuer ist natürlich sowohl für NiMH als auch für Li-Ion eine ganz schlechte Idee. Lasst da die Finger von]. Beides ist weniger als ein laues Lüftchen gegen die Energiedichte eines Schmelzsalzreaktors.

    Was schließlich auf den zentralen Grund führt, warum mensch Nukleartechnologie in so wenigen Händen wie möglich haben will: Sie ist ein riesiger Hebel. Es gibt fast nichts anderes, mit dem ein einzelner, entschlossener Mensch eine Million andere Menschen umbringen kann. Ein Kilo Plutonium-239, geeignet verteilt, reicht jedenfalls mal, um die alle ordentlich zu verstahlen (nämlich den Jahres-Grenzwert für die Inhalation von α-Strahlern um einen Faktor 25 zu überschreiten). Ein paar Kilo Uran-232 (wie es sich aus Thorium-Brütern – und die braucht es von den Rohstoffreserven her, wenn der Kram eine Rolle bei der Gesamtenergieversorgung spielen soll – gewinnen lässt) reichen für eine richtige Bombe, die mechanisch so einfach ist, dass sie einE entschiedeneR BastlerIn hinkriegen kann. Dieser Hebel ist übrigens nicht nur für sich problematisch; er ist auch der Grund, warum ein Staat in Gegenwart verbreiteter Nukleartechnologie praktisch autoritär werden muss (vgl. Robert Jungks Atomstaat [2]), einfach weil er den Hebel so intensiv bewachen muss.

    Allein wegen dieses riesigen Hebels und der Tatsache, dass Leute auch ohne den gegenwärtigen Modetrend Faschismus immer mal wieder durchknallen will mensch hohe Neutronendichten nicht im Zugriff vieler Menschen haben. Und das heißt: AKWs im breiten, kommerziellen Einsatz [3] sind ein Rezept für Massenmord und autoritäre Staaten.

    Es gibt eigentlich nur eine Technologie, die einen noch größeren Hebel hat: Das ist DNA-Basteln. Mir schaudert vor der Zeit, in der die Leute, die heute Erpressungstrojaner schreiben, die Übertragbarkeit von Windpocken mit der Tödlichkeit der Masernfamilie zusammenprogrammieren und das Ergebnis mit DNA-Druckern und Bioreaktoren in diese Welt bringen können.

    [1]Höchst lesenswertes Buch in diesem Zusammenhang: Hilgartner, S, Bell, R.C., O'Connor, R.: Nukespeak – the selling of nuclear technology in America, Penguin Books 1982. Gibts leider nicht in der Imperial Library, aber dann und wann noch antiquarisch.
    [2]Gibts leider auch nicht in der Imperial Library.
    [3]Wer findet, dass ich hier defensiv klinge: Ja, na ja, ganz ohne erbrütete Radionuklide müssten wir die ganzen Nuklearmedizinabteilungen dichtmachen, und das wäre zumindest in Einzelfällen schon schade. Vielleicht reichen für sowas Spallationsquellen, aber wenn nicht: zwei, drei kleine Reaktoren weltweit wären jedenfalls genug; viel mehr ist es auch heute nicht, was den Krankenhausbedarf an wilden Isotopen deckt.

  • Unübersehbare Konsequenzen

    12021:112:0 ( 2021-04-22)

    Als ich gestern endlich mal die autoritäre Versuchung in einiger Breite diskutiert habe, war eines der Argumente gegen die bequeme Lösung von Konflikten mit Zwang und Gewalt, dass diese Lösungen zwar manchmal den erwünschten Effekt haben, aber in der Regel auch ziemlich haarsträubende Nebenwirkungen.

    Blätter und Stängel

    Hydrilla-Pflanzen in einem Foto vom US Geological Survey.

    Dazu ist mir heute in einem Beitrag zu Forschung aktuell vom 26. März ein relativ exotisches Beispiel untergekommen, allerdings ziemlich weit ab von den sozialen Konflikten, über die ich gestern vor allem geschrieben habe. Es ging in der Sendung um ein aktuelles Science-Paper von Steffen Breinlinger, Tabitha Phillips und KollegInnen (DOI 10.1126/science.aax9050). Die Leute haben untersucht, warum ab Mitte der 1990er in bestimmten Gebieten der südlichen USA eine deutliche Übersterblichkeit von Weißkopf-Seeadlern und, bei näherem Hinsehen, entlang ganzer Nahrungsketten in und über Süßwasserseen auftrat.

    Zunächst war schon vor der Arbeit eine Korrelation der toten Vögel mit der Besiedlung von Seen durch Hydrilla (eine dort vom Menschen vor relativ kurzer Zeit aus der alten Welt eingeführte Wasserpflanze) aufgefallen, genauer durch Hydrilla und ein Cyanobakterium, das auf dieser haust. Das Weitere hatte etwas von einer Sherlock Holmes-Geschichte, denn Nachzucht und Verfütterung des Cyanobakteriums waren ein Haufen Arbeit – und führten zu nichts: Tiere, die den Hydrilla-Cyanobakterien-Cocktail verzehrten, fühlten sich prima.

    Erst mit echtem Pamp aus den todbringenden Seen erkannten die WissenschaftlerInnen, dass das Problem nicht das Cyanobakterium an sich war, sondern im Wesentlichen die Fähigkeit von Hydrilla, Brom anzureichern; erst mit wenigstens etwas Kaliumbromid im Wasser und Hydrilla zur Bromid-Anreicherung wurden die Cyanobaktierien giftig.

    Damit stellt sich die Frage, woher die Bromide in der freien Natur kommen. Und da kommen wir zu den autoritären Lösungen. Hydrilla ist invasiv, breitet sich also ziemlich stark aus, seit jemand mal sein Aquarium in einen See gekippt und die Pflanze so in die Gewässer der südlichen USA gebracht hat. Um der Ausbreitung Herr zu werden, wurde wohl teils auf Herbizide zurückgegriffen, die bromierte Kohlenwasserstoffe enthielten.

    Tja: Da hat wohl wer einer autoritären Versuchung nachgegeben und die einfache Lösung gesucht durch, na ja, das nächste Aquivalent zu Gewalt an Pflanzen. Vermutlich hat das nicht mal besonders gut gegen Hydrilla geholfen – es muss ja noch genug davon gegeben haben, dass Tiere durch Abweiden (bzw. Fressen der Abweidenden) das Cyanobakterien-Gift anreichen konnten. Aber plausiblerweise hat das Herbizid, die „Lösung“, am Schluss die Seeadler (und Eulen und Milane) umgebracht.

    Der Fairness halber: Vielleicht wars auch gar nichts in der Richtung. Brom könnte auch aus weggeworfenem Kram mit Flammschutzmitteln (das waren traditionell halogenierte Kohlenwasserstoffe) oder aus der Reinigung von Abgasen der Kohleverstromung kommen. Und klar, es gibt auch natürliche Vorkommen von Bromverbindungen. So ist das halt mit Wissenschaft: Richtig eindeutige Antworten brauchen lange Zeit.

  • Worse is manchmal better

    12021:094:9 ( 2021-04-05)

    TL;DR: Radikalität ist wichtig, aber Freundlichkeit ist wichtiger.

    Seit einiger Zeit blättere ich öfter mal in Shoshana Zuboffs Age of Surveillence Capitalism und finde es immer wieder nützlich und gleichzeitig verkehrt. Dazu will ich etwas mehr schreiben, wenn ich es ganz gelesen habe, aber jetzt gerade hat mich ihr Generalangriff auf den Behaviorismus – auch der gleichzeitig richtig und falsch – wieder an einen Gedanken aus Bertrand Russells A History of Western Philosophy erinnert, der mich immer wieder beschäftigt – und den ich sehr profund finde. Im Groben: „In politischen Theorien ist Menschlichkeit wichtiger als Stringenz”. Oder: das „worse is better“ der Unix-Philosophie, das mensch trefflich kritisieren kann, ist zumindest fürs politische Denken in der Regel angemessen.

    Was ist eigentlich eine Menge?

    Foto eines Computers

    Gegenstück zu worse is better: Eine LISP-Maschine im MIT-Museum.

    Dabei konnte Russell beeindruckend stringent denken, etwa auf den paar hundert Seiten, die er in den Principia Mathematica füllte, um sich der Richtigkeit von 1+1=2 zu versichern.

    Oder auch in der Russell'schen Antinomie, die ich in meinen Einführungsvorlesungen in die formalen Grundlagen der Linguisitk immer zur Warnung vor der naiven Mengendefinition – eine Menge sei ein Haufen von „Objekten unserer Anschauung oder unseres Denkens“ – gebracht habe. Wäre diese Definition nämlich ok, müsste es auch die Menge aller Mengen geben, die sich nicht selbst enthalten. Nennen wir sie mal Ξ (ich finde, das große Xi ist in Mathematik und Physik deutlich unterverwendet). Die wesentliche Frage, die mensch einer Menge stellen kann ist: Ist irgendwas in dir drin, also: „x ∈ Ξ“?

    Und damit kommt Russells geniale Frage: Ist Ξ ∈ Ξ oder nicht? Schauen wir mal:

    • Wenn Ξ ∈ Ξ gälte, enthält Ξ sich selbst, ist also nicht in der Mengen aller Mengen, die sich nicht selbst enthalten, entgegen der Annahme in diesem Spiegelstrich.
    • Ist aber Ξ ∉ Ξ, so enthält sich Ξ nicht selbst, wäre es also in der Menge aller Mengen, die sich nicht selbst enthalten und müsste sich also selbst enthalten. Passt wieder nicht.

    Brilliant, oder? Die Lösung dieser „Russell'schen Antinomie“ ist übrigens, sich bei der Definition von „Menge“ etwas mehr Mühe zu geben.

    Wer das nachvollzogen hat, wird wohl die Weisheit von Russells Entscheidung erkennen, nach den Principia Mathematica eher konventionelle Philosophie zu betreiben. In diesem Rahmen hat er 1945 seine überaus lesbare Darstellung der „westlichen“ Philosophie veröffentlicht, in der er sich deutlich als Fan von John Locke outet, den „apostle of the Revolution of 1688, the most moderate and the most successful of all revolutions“, erfolgreichst, denn „no subsequent revolution has hitherto been found necessary in England.“ Über das „found necessary“ könnte mensch angesichts des Elends, das noch in den Werken von George Orwell – geschrieben, während Russell in den 1940ern an seiner History arbeitete – deutlich wird, sicher streiten, aber vielleicht ist das durch „most moderate“ noch hinreichend abgedeckt.

    Vernünftig vs. Widerspruchsfrei in der politischen Doktrin

    Viel wichtiger ist mir aber Russells Beobachtung: „Pragmatically, the theory was useful, however mistaken it may have been theoretically. This is typical of Locke's doctrines.“ Etwas später sagt er: „No one has yet succeeded in inventing a philosophy at once credible and self-consistent. Locke aimed at credibility, and achieved it at the expense of consistency. Most of the great philosophers have done the opposite.“

    Also in etwa: in der Philosophie – und da würde ich etwas hinter Russell zurückgehen wollen und sagen: Politik und Soziologie – gibt es nicht gleichzeitig „glaubwürdig“ (sagen wir lieber: menschlich) und widerspruchsfrei. Ich glaube, Russell kam zu diesem desillusionierten Einsichten aus Enttäuschung mit der russischen Revolution, deren Scheitern, jedenfalls im Sinne von Freiheit, Gleichheit und Solidarität für die Bürger_innen der Sowjetunion, er wahrscheinlich mit übermäßiger ideologischer Strenge erklärte; jedenfalls führte er Lockes gedankliche Geschmeidigkeit zurück auf dessen Erfahrungen des britischen Bürgerkriegs der 1640er Jahre.

    Immer wieder spottet Russell freundlich über Lockes, nun, Liberalität, so etwa, wenn Hume einen schlimmen Irrtum beging, weil er „a better intellect than Locke's, a greater acuteness in analysis, and a smaller capacity for accepting comfortable inconsistencies“ hat. Oder wenn er Lockes Methode so umschreibt:

    [Er ist] always willing to sacrifice logic rather than become paradoxical. He enunciates general principles which, as the reader can hardly fail to perceive, are capable of leading to strange consequences; but whenever the strange consequences seem about to appear, Locke blandly refrains from drawing them. To a logician this is irritating; to a practical man, it is a proof of sound judgement.

    Was ich daraus mache: Wenn du über die Gesellschaft nachdenkst und du kommst auf Menschenfresserei, müssen deine Ausgangsgedanken nicht unbedingt Quatsch sein – das kann schon mal passieren, wenn ein Haufen Leute sich streiten. Du solltest aber trotzdem nicht Menschenfresser_in werden.

    Freundlichkeit vs. Radikalität in der politischen Praxis

    Eine derzeit ganz naheliegende Anwendung: So sehr es scheiße ist, wenn Leute an eigentlich vermeidbaren Krankheiten sterben: Die autoritäre Fantasie, einfach alle einzusperren, bis die SARS-2-Pandemie vorbei ist, ist schon deshalb nicht menschenfreundlich, weil so ein Präzedenzfall zu inflationären Forderungen nach ähnlich autoritären Maßnahmen führen wird (alles andere mal beiseitegelassen). Umgekehrt führt das unbedingte Bestehen auf Grundrechten wie Freizügigkeit, die Zurückweisung staatlicher Autorität, auch wo diese nicht immer so richtig wissenschaftlich unterfüttert ist, zu einem schlimmen Gemetzel. Es bleibt, sich da irgendwie durchzumogeln (und das, ich gebs immer noch nicht gerne zu, hat die Regierung recht ordentlich gemacht), und das ist wohl, was was Russell an Locke mag.

    Also: Im realen Umgang mit Menschen ist Freundlichkeit oft wichtiger als Konsequenz. Dass Russell, obwohl er fast jeden Gedanken von Locke widerlegt, seine gesamte Lehre sehr wohlwollend betrachtet, ist eine sozusagen rekursive Anwendung dieses Prinzips.

    Leider, und da kommen wir beinahe auf die Russell'sche Antinomie zurück, bin ich aber überzeugt, dass auch die Mahnung, es mit den Prinzipien nicht zu weit zu treiben, dieser Mahnung selbst unterliegt. Folterverbot oder Ausschluss der Todesstrafe etwa würde ich gerne unverhandelbar sehen.

    Locke hätte mit dieser fast-paradoxen Selbstanwendung von Nicht-Doktrinen auf Nicht-Doktrinen bestimmt keine Probleme gehabt. Bei mir bin ich mir noch nicht ganz sicher.

    Aber ich versuche, Zuboff mit der Sorte von Wohlwollen zu lesen, die Russell für Locke hatte.

    Nachtrag (2021-04-10)

    Weil ich gerade über irgendeinen Twitter-Aktivismus nachdenken musste (bei dem jedenfalls für mein Verständnis allzu oft gute Absichten zu böser Tat werden), ist mir aufgefallen, dass meine Russell-Interpretation eigentlich zusammenzufassen ist mit: „Radikalität ist wichtig, aber Freundlichkeit ist wichtiger“. Das hat mir auf Anhieb gefallen, weshalb ich es auch gleich als TL;DR über den Artikel gesetzt habe.

    Dann habe ich geschaut, ob duckduckgo diesen Satz kennt. Erstaunlicherweise nein. Auch bei google: Fehlanzeige. Ha!

    Und je mehr ich darüber nachdenke, gerade auch im Hinblick auf ein paar Jahrzehnte linker Politik: RiwaFiw hätte vieles besser gemacht, und, soweit ich sehen kann, fast nichts schlechter.

  • Die Viren loben

    12021:091:6 ( 2021-04-02)

    „Jetzt ist aber wirklich höchste Zeit, dass Corona endlich mal weggeht“ ist inzwischen ein universelles Sentiment, und auch mich lockt gelegentlich die autoritäre Versuchung, einen „harten Lockdown“ zu wünschen, damit das Ding weggeht (was es natürlich nicht täte). Der Hass auf SARS-2 steigt, und damit womöglich auf Viren allgemein.

    In der Tat scheinen Viren erstmal richtig doof, eklig und widerwärtig. Wie scheiße ist das eigentlich, sich von den Zellen vertrauensvoll aufnehmen zu lassen und dann den Laden zu übernehmen mit dem einzigen Ziel, neues Virus zu machen? Und dann die Ähnlichkeit von z.B. der T2-Bakteriophage mit Invasoren vom Mars...

    Andererseits bin ich überzeugt, dass eine gewisse Anfälligkeit gegen Viren wahrscheinlich ein evolutionärer Vorteil ist. Da gibts bestimmt jede Menge echte Wissenschaft dazu, aber ich denke, eine einfache Intiution geht auch ohne: Praktisch alle Viren nämlich wirken nur auf kurze Distanz in Zeit und Raum (verglichen etwa mit Pflanzenpollen, aber sogar mit vielen Bakterien), werden also im Wesentlichen bei Begegnungen übertragen. Da die Wahrscheinlichkeit von Begegnungen mit dem Quadrat der Bevölkerungsdichte geht, sollten Viren explodierende Populationen „weicher“ begrenzen als leergefressene Ressourcen und so wahrscheinlich katastrophalen Aussterbeereignissen vorbeugen.

    Vorneweg: Ja, das klingt alles erstmal wild nach Thomas Malthus. Dessen Rechtfertigung massenhaften Sterbenlassens ist natürlich unakzeptabel (ebenso allerdings wie das fortgesetzte Weggucken von den Meadows-Prognosen, die in der Regel auch katastrophale Zusammenbrüche erwarten lassen).

    Dies aber nicht, weil falsch wäre, dass in endlichen Systemen der Ressourcengebrauch nicht endlos steigen kann; das ist nahe an einer Tautologie. Nein, Malthus' Fehler ist der der Soziobiologie, nämlich menschliche Gesellschaft und menschliches Verhalten an Funktionsweisen der Natur auszurichten. Wer das will, wird recht notwendig zum Schlächter, während umgekehrt die Geschichte der letzten 100 Jahre überdeutlich zeigt, wie (sagen wir) Wachstumszwänge diverser Art durch mehr Bildung, mehr Gleichheit und vor allem durch reproduktive Selbstbestimmung von Frauen ganz ohne Blutbad und unter deutlicher Hebung der generellen Wohlfahrt zu beseitigen sind.

    Bei Kaninchen ist das aber, da muss ich mich leider etwas als Speziezist outen, anders. Und daher habe ich mir Modellkaninchen für ein weiteres meiner Computerexperimente herausgesucht, ganz analog zu den Schurken und Engeln.

    Die Fragestellung ist: Werden Ausschläge in Populationen wirklich weniger wild, wenn Viren (also irgendwas, das Individuen nach Begegnungen mit einer gewissen Wahrscheinlichkeit umbringt) im Spiel sind?

    Um das zu untersuchen, baue ich mir eine Spielwelt (wer mag, kann auch „modifiziertes Lotka-Volterra-Modell“ dazu sagen) wie folgt:

    • Es gibt 1000 Felder, auf denen Gras wachsen kann oder nicht.
    • In der Welt leben Kaninchen, die pro Periode ein Grasfeld leerfressen müssen, damit sie glücklich sind.
    • Haben Kaninchen mehr Gras als sie brauchen, vermehren sie sich, und zwar um so mehr, je mehr Extrafutter sie haben (so machen das zumindest Rehe).
    • Haben Kaninchen zu wenig Gras, sterben ein paar.
    • In jeder Periode verdoppelt sich die Zahl der Grasfelder (sagen wir: durch Aussaat), bis alle 1000 Felder voll sind.

    In Code sieht die Berechnung der Vermehrungsrate der Kaninchen so aus:

    def get_growth_factor(self):
  grass_per_rabbits = self.grass/self.rabbits
  if grass_per_rabbits<1:
    return grass_per_rabbits**2
  else:
    return 1+math.sqrt(grass_per_rabbits-1)

    Wer den Verlauf der Vermehrungsrate mit dem Gras/Kaninchenverhältnis γ auf der Abszisse sehen will:

    Um dieses Modell zu rechnen, habe ich ein kleines Python-Programm geschrieben, lv.py, das, mit anfänglichen Zahlen von Gras und Kaninchen aufgerufen, den Verlauf der jeweiligen Populationen im Modell ausgibt (nachdem es die Anfangsbedingungen etwas rausevolvieren hat lassen).

    Wie bei dieser Sorte von Modell zu erwarten, schwanken die Populationen ziemlich (außer im Fixpunkt Kaninchen=Gras). So sieht das z.B. für python3 lv.py 400 410 (also: anfänglich ziemlich nah am Gleichgewicht) aus:

    Das sieht nicht viel anders aus, wenn ich mit einem Kaninchen-Überschuss anfange (python3 lv.py 400 800):

    oder mit einem Gras-Paradies (python3 lv.py 800 150):

    Aus Modellsicht ist das schon mal fein: Recht unabhängig von den Anfangsbedingungen (solange sie im Rahmen bleiben) kommen zwar verschiedene, aber qualitativ doch recht ähnliche Dinge raus: die Kaninchenpopulationen liegen so zwischen 250 und 600 – im anfänglichen Gras-Paradies auch mal etwas weiter auseinander – und schwanken wild von Schritt zu Schritt.

    Jetzt baue ich einen Virus dazu. Im lv.py geht das durch Erben vom LV-Modell, was auf die LVWithVirus-Klasse führt. Diese hat einen zusätzlichen Parameter, deadliness, der grob sagt, wie wahrscheinlich es ist, dass ein Kaninchen nach einer Begegnung mit einem anderen Kaninchen stirbt. Die Mathematik in der propagate-Methode,

    def propagate(self):
  LV.propagate(self)
  self.rabbits = max(1, self.rabbits-self.rabbits**2*self.deadliness)

    würde etwa einem Bau entsprechen, in dem sich alle Kaninchen ein Mal pro Periode sehen. Das ist jetzt sicher kein gutes Modell für irgendwas, aber es würde mich sehr überraschen, wenn die Details der Krankheitsmodellierung viel an den qualitativen Ergebnissen ändern würden. Wichtig dürfte nur sein, dass die Todesrate irgendwie überlinear mit der Population geht.

    lv.py lässt das Modell mit Virus laufen, wenn es ein drittes Argument, also die Tödlichkeit, bekommt. Allzu tödliche Viren löschen die Population aus (python3 lv.py 800 150 0.05):

    Zu harmlose Viren ändern das Verhalten nicht nennenswert (python3 lv.py 800 150 1e-6):

    Interessant wird es dazwischen, zum Beispiel python3 lv.py 800 150 2.1e-4 (also: rund jede fünftausendste Begegnung bringt ein Kaninchen um):

    – wer an die Beschriftung der Ordinate schaut, wird feststellen, dass die Schwankungen tatsächlich (relativ) kleiner geworden sind. Das Virus wirkt offenbar wirklich regularisierend.

    Wir befinden uns aber im Traditionsgebiet der Chaostheorie, und so überrascht nicht, dass es Bereiche der Tödlichkeit gibt, in denen plötzlich eine starke Abhängigkeit von den Anfangsbedingungen entsteht und sich die Verhältnisse weit in die Entwicklung rein nochmal grundsätzlich ändern können („nicht-ergodisch“). So etwa python3 lv.py 802 300 0.0012:

    gegen python3 lv.py 803 300 0.0012:

    Ein Kaninchen weniger am Anfang macht hundert Schritte später plötzlich so ein gedrängeltes, langsames Wachstum.

    Warum ich gerade bei 0.0012 geschaut habe? Nun ich wollte einen Überblick über das Verhalten bei verschiedenen Tödlichkeiten und habe darum stability_by_deadliness.py geschrieben, das einfach ein paar interessante Tödlichkeiten durchprobiert und dann die relative Schwankung (in Wirklichkeit: Standardabweichung durch Mittelwert) und den Mittelwert der Population über der Virustödlichkeit aufträgt:

    – das sieht sehr gut aus für meine These: Mit wachsender Tödlichkeit des Virus nimmt die relative Streuung der Population ab, irgendwann allerdings auch die Population selbst. Ganz links im Graphen gehts durcheinander, weil sich dort chaotisches Systemverhalten mit kleinen Zahlen tifft, und dazwischen scheint es noch ein, zwei Phasenübergänge zu geben.

    Leider ist dieses Bild nicht wirklich robust. Wenn ich z.B. die Anfangsbedingungen auf 600 Gras und 250 Kaninchen ändere, kommt sowas raus:

    – die meisten der Effekte, die mich gefreut haben, sind schwach oder gar ganz weg – wohlgemerkt, ohne Modelländerung, nur, weil ich zwei (letztlich) Zufallszahlen geändert habe.

    Mit etwas Buddeln findet mensch auch das Umgekehrte: wer immer mit 170 Gras und 760 Kaninchen anfängt, bekommt einen Bereich, in dem die Populationen mit Virus größer sind als ohne, während gleichzeitig die relative Schwankung nur noch halb so groß ist wie ohne Virus. Dazwischen liegt ein 1a Phasenübergang:

    Mensch ahnt: da steckt viel Rauschen drin, und auf der anderen Seite höchst stabiles Verhalten, wo mensch es vielleicht nicht erwarten würde (bei den hohen Tödlichkeiten und mithin kleinen Zahlen). Wissenschaft wäre jetzt, das systematisch anzusehen (a.k.a. „Arbeit“). Das aber ist für sehr ähnliche Modelle garantiert schon etliche Male gemacht worden, so dass der wirklich erste Schritt im Jahr 51 nach PDP-11 erstmal Literatur-Recherche wäre.

    Dazu bin ich natürlich zu faul – das hier ist ja nicht mein Job.

    Aber das kleine Spiel hat meine Ahnung – Viren stabilisieren Ökosysteme – weit genug gestützt, dass ich weiter dran glauben kann. Und doch wäre ich ein wenig neugierig, was die Dynamische-Systeme-Leute an harter Wissenschaft zum Thema zu bieten haben. Einsendungen?

  • Tintenfische und der Erfolg im Leben

    12021:085:1 ( 2021-03-26)
    Ein Oktopus im Porträt

    Gut: Es ist keine Sepie. Aber dieser Oktopus ist bestimmt noch viel schlauer.

    Mal wieder gab es in Forschung aktuell ein Verhaltensexperiment, das mich interessiert hat. Anders als neulich mit den Weißbüschelaffen sind dieses Mal glücklicherweise keine Primaten im Spiel, sondern Tintenfische, genauer Sepien – die mir aber auch nahegehen, schon, weil das „leerer Tab“-Bild in meinem Browser eine ausgesprochen putzige Sepie ist. Den Beitrag, der mich drauf gebraucht hat, gibt es nur als Audio (1:48 bis 2:28; Fluch auf die Zeitungsverleger), aber dafür ist die Original-Publikation von Alexandra Schnell et al (DOI 10.1098/rspb.2020.3161) offen.

    Grober Hintergrund ist der Marshmallow-Test. Bemerkenswerterweise zitiert der Wikipedia-Artikel bereits die Sepien-Publikation, nicht jedoch kritischere Studien wie etwa die auf den ersten Blick ganz gut gemachte von Watts et al (2018) (DOI: 10.1177/0956797618761661). Schon dessen Abstract nimmt etwas die Luft aus dem reaktionären Narrativ der undisziplinierten Unterschichten, die selbst an ihrem Elend Schuld sind:

    an additional minute waited at age 4 predicted a gain of approximately one tenth of a standard deviation in achievement at age 15. But this bivariate correlation was only half the size of those reported in the original studies and was reduced by two thirds in the presence of controls for family background, early cognitive ability, and the home environment. Most of the variation in adolescent achievement came from being able to wait at least 20 s. Associations between delay time and measures of behavioral outcomes at age 15 were much smaller and rarely statistically significant.

    Aber klar: „achievement“ in Zahlen fassen, aus denen mensch eine Standardabweichung ableiten kann, ist für Metrikskeptiker wie mich auch dann haarig, wenn mich die Ergebnisse nicht überraschen. Insofern würde ich die Watts-Studie jetzt auch nicht überwerten. Dennoch fühle ich mich angesichts der anderen, wahrscheinlich eher noch schwächeren, zitierten Quellen eigentlich schon aufgerufen, die Wikipedia an dieser Stelle etwas zu verbessern.

    Egal, die Tintenfische: Alexandra Schnell hat mit ein paar Kolleg_innen in Cambridge also festgestellt, dass Tintenfische bis zu zwei Minuten eine Beute ignorieren können, wenn sie damit rechnen, später etwas zu kriegen, das sie lieber haben – und wie üblich bei der Sorte Experimente ist der interessanteste Teil, wie sie es angestellt haben, die Tiere zu irgendeinem Handeln in ihrem Sinn zu bewegen.

    Süß ist erstmal, dass ihre ProbandInnen sechs Tintenfisch-Jugendliche im Alter von neun Monaten waren. Die haben sie vor einen Mechanismus (ebenfalls süß: Die Autor_innen finden den Umstand, dass sie den 3D-gedruckt haben, erwähnenswert genug für ihr Paper) mit zwei durchsichtigen Türen gesetzt, hinter denen die Sepien jeweils ihre Lieblingsspeise und eine Nicht-so-Lieblingsspeise (in beiden Fällen irgendwelche ziemlich ekligen Krebstiere) sehen konnten. Durch irgendwelche Sepien-erkennbaren Symbole wussten die Tiere, wie lange sie würden warten müssen, bis sie zur Leibspeise kommen würden, zum langweiligen Essen konnten sie gleich, und sie wussten auch, dass sie nur einen von beiden Ködern würden essen können; dazu gabs ein recht durchdachtes Trainingsprotokoll.

    Na ja, in Wirklichkeit wars schon etwas komplizierter mit dem Training, und ahnt mensch schon, dass nicht immer alles optimal lief:

    Preliminary trials in the control condition showed that Asian shore crabs were not a sufficiently tempting immediate reward as latencies to approach the crab, which was baited in the immediate-release chamber, were excessive (greater than 3 min) and some subjects refused to eat the crab altogether.

    Ich kann mir richtig vorstellen, wie die Gruppe vor dem Aquarium stand und fluchte, weil die doofen Viecher ihre Köder nicht schlucken wollten: „Wie zum Henker schreiben wir das nachher ins Paper?“ – um so mehr, als alle Sepien konsequent die gleichen Präferenzen hatten (was ich ja auch schon für ein bemerkenswertes Resultat halte, das bei n=6 und drei Auswahlmöglichkeiten kaum durch Zufall zu erklären ist – vielleicht aber natürlich durch das, was die Sepien sonst so essen).

    Und dann wieder Dinge in der Abteilung „was alles schiefgehen kann, wenn mensch mit Tieren arbeitet“:

    Subjects received one session of 6 trials per day at a specific delay. This number of trials was chosen to minimize satiety and its effects on eating behaviour.

    Schon die Abbildung 2 des Artikels finde ich wirklich erstaunlich: Alle Sepien bekommen es hin, 30 Sekunden auf ihre Lieblingsspeise zu warten – wow. Ok, kann natürlich sein, dass sie so lange brauchen, um sich zu orientieren, aber Schnell und Co scheinen mir schon viel getan zu haben, um das unwahrscheinlich zu machen.

    Was jedenfalls rauskommen sollte, war eine Korrelation der Wartezeit mit, na ja, der „Intelligenz“ (ich halte mich raus bei der genaueren Bestimmung, was das wohl sei), und um die zu messen, mussten die Sepien in ihren Aquarien zunächst lernen, das „richtige“ unter einem dunklen und einem hellen Stück Plastik aussuchen. Anschließend, das war der Intelligenztest, mussten sie mitbekommen, wenn die Versuchsleitung die Definition von „richtig“ verändert hat. Dazu haben sie laut Artikel im Mittel 46 Versuche gebraucht – gegenüber 27 Versuchen beim ersten Lernen. Nicht selbstverständlich auch: Sepien, die beim ersten Lernen schneller waren, waren auch schneller beim Begreifen der Regeländerung. Da ist Abbildung 3 schon ziemlich eindrücklich: einer der Tintenfische hat das Umkehrlernen in gut 20 Schritten bewältigt, ein anderer hat fast 70 Schritte gebraucht. Uiuiui – entweder haben die ziemlich schwankende Tagesform, oder die Gerissenheit von Sepien variiert ganz dramatisch zwischen Individuen.

    Die erwartete Korrelation kam selbstverständlich auch raus (Abbildung 4), und zwar in einer Klarheit, die mich schon etwas erschreckt angesichts der vielen Dinge, die beim Arbeiten mit Tieren schief gehen können; der Bayes-Faktor, den sie im Absatz drüber angeben („es ist 8.83-mal wahrscheinlicher, dass Intelligenz und Wartenkönnen korreliert sind als das Gegenteil“) ist bei diesem Bild ganz offensichtlich nur wegen der kleinen Zahl der ProbandInnen nicht gigantisch groß. Hm.

    Schön fand ich noch eine eher anekdotische Beobachtung:

    [Andere Tiere] have been shown to employ behavioural strategies such as looking away, closing their eyes or distracting themselves with other objects while waiting for a better reward. Interestingly, in our study, cuttlefish were observed turning their body away from the immediately available prey item, as if to distract themselves when they needed to delay immediate gratification.

    Ich bin vielleicht nach der Lektüre des Artikels nicht viel überzeugter von den verschiedenen Erzählungen rund um den Marshmallow-Test.

    Aber ich will auch mit Sepien spielen dürfen.

  • Schurken und Engel, Teil 2

    12021:072:7 ( 2021-03-14)

    Ich bin gestern nochmal der Sache mit den Schurken und Engeln von neulich nachgegangen, denn auch wenn die grundsätzliche Schlussfolgerung – wenn du Chefposten kompetetiv verteilst, kriegst du ziemlich wahrscheinlich Schurken als Chefs – robust ist und ja schon aus der dort gemachten qualitativen Abschätzung folgt, so gibt es natürlich doch jede Menge interessante offene Fragen: Setzen sich Schurken drastischer durch wenn die Engeligkeit steiler verteilt ist? Wie sehr wirkt sich der Vorteil für die Schurken wirklich aus, vor allem, wenn sie auch nur eine endliche Lebensdauer haben? Wie ändern sich die Ergebnisse, wenn Leute zweite und dritte Chancen bekommen, mal wie ein richtiger Schurke Karriere zu machen? Wie verändert sich das Bild, wenn mensch mehr Hierarchiestufen hinzufügt?

    Weil das alte Modell mit der einen Kohorte, die bei jedem Schritt um den Faktor 2 eindampft, für solche Fragen zu schlicht ist, muss ein neues her. Es hat den Nachteil, dass es viel mehr Code braucht als das alte – es hat aber der Vorteil, dass es im Prinzip beliebig lang laufen kann und über einen weiten Bereich von Parametern hinweg stationär werden dürfte, sich also der Zustand nach einer Weile (der „Relaxationszeit“) nicht mehr ändern sollte – natürlich vom Rauschen durch die diskrete Simulation abgesehen. Wem also das alte Modell zu schlicht und langweilig ist: Hier ist sunde2.py.

    Das Neue

    Wie sieht das Modell aus? Nun, wir haben jetzt simultan einen ganzen Haufen N von Hierarchiestufen, die auch immer alle besetzt sind; derzeit habe ich konstant N = 50. Von Stufe zu Stufe ändert sich jetzt die Population nicht mehr je um einen Faktor zwei, sondern so, dass die unterste Stufe 16-mal mehr Aktoren hat als die oberste und die Besetzungszahl dazwischen exponentiell geht. Diese Schicht-Statistik sollte keinen großen Einfluss auf die Ergebnisse haben, hält aber einerseits die Zahl der zu simulierenden Aktoren auch bei tiefen Hierarchien im Rahmen, ohne andererseits auf den oberen Ebenen die ganze Zeit mit allzu kleinen Zahlen kämpfen zu müssen.

    Aktoren haben jetzt auch ein Alter; sie sterben (meist) nach L ⋅ N Runden; L kann interpretiert werden als die Zahl der Versuche pro Wettbewerb, die ein Aktor im Mittel hat, wenn er ganz nach oben will. Im Code heißt das lifetime_factor (hier: Lebenzeit-Faktor), und ich nehme den meist als 2 („vita brevis“).

    Es gibt eine Ausnahme auf der strikten Lebenszeitbegrenzung: Wenn ein Level sich schon um mehr als die Hälfte geleert hat, überleben die, die noch drin sind, auch wenn sie eigentlich schon sterben müssten. An sich ist diese künstliche Lebensverlängerung nur ein technischer Trick, damit mir der Kram mit ungünstigen Parametern und bei der Relaxation nicht auf interessante Weise um die Ohren fliegt; es kann nämlich durchaus sein, dass die oberen Ebenen „verhungern“, weil Aktoren schneller sterben als befördert werden. Er hat aber den interessanten Nebeneffekt, dass speziell in Modellen mit kleinem L wie in der Realität die Lebenserwartung der höheren Klassen höher ist als die der unteren.

    Um die Gesamtzahl der Aktoren konstant zu halten, werden in jeder Runde so viele Aktoren geboren wie gestorben sind, und zwar alle in die niedrigste Schicht.

    Das enspricht natürlich überhaupt nicht der Realität – schon die Zahlen zur Bildungsbeteiligung gegen Ende des Posts Immerhin gegen Ende zeigen ja, dass viele Menschen mitnichten bei Null anfangen in ihrem gesellschaftlichen Aufstieg. Insofern hätte mensch darüber nachdenken können, bestehende Aktoren irgendwie fortzupflanzen. Das aber hätte eine Theorie zum Erbgang von Schurkigkeit gebraucht (die auch dann nicht einfach ist, wenn mensch wie ich da wenig oder keine biologische Komponenten vermutet) und darüber hinaus den Einbau von Abstiegen in der Hierarchie erfordert.

    Die zusätzliche Komplexität davon wäre jetzt nicht dramatisch gewesen, aber das kontrafaktische „alle fangen bei Null an“ residiert als „Chancengleichheit“ auch im Kern der modernen Wettbewerbsreligion. Für ein Modell – das ohnehin in einer eher lockeren Beziehung zur Wirklichkeit steht – ist sie daher genau richtig. Sollten übrigens in der Realität Kinder von eher schurkigen Menschen auch tendenziell eher schurkig werden, würde das die Anreicherung von Schurkigkeit gegenüber dem chancengleichen Modell nur verstärken.

    Das Alte

    Der Rest ist wie beim einfachen Modell: da es gibt den Schurken-Vorteil, die Wahrscheinlichkeit, dass ein Aktor, der gerade schurkig ist, gegen einen, der gerade engelig ist, gewinnt. Dieser rogue_advantage ist bei mir in der Regel 0.66.

    Der letzte Parameter ist die Verteilung der Schurkigkeit (also der Wahrscheinlichkeit, dass sich ein Aktor in einem Wettbewerb als Schurke verhält). Dazu habe ich wie zuvor eine Gleichverteilung, Exponentialverteilungen der Schurkigkeit mit verschidenen λ (also: gegenüber der Gleichverteilung sind mehr Aktoren Engel, wobei die allerdings alle Schurkeigkeiten über 1 auf 1 beschnitten werden; für kleine λ wird das also schwer zu interpretieren) und Normalverteilungen reingebaut, dieses Mal aber viel expliziter als im einfachen Modell des letzten Posts.

    Ich hatte eigentlich vor, den Kram immer laufen zu lassen, bis er „stationär“ würde, also sagen wir, bis der Schurkigkeits-Gradient in den mittleren Schichten sich von Runde zu Runde nicht mehr wesentlich ändert. Stellt sich aber raus: durch die relativ überschaubaren Aktor-Zahlen und die Dynamik der Gesellschaft, in der ja per Design viel Aufstieg stattfindet, rauschen die Metriken, die ich da probiert habe, zu stark, um guten Gewissens sagen zu können, jetzt sei das Ding relaxiert (im Code: DiffingWatcher).

    Was passiert?

    Stattdessen lasse ich die Modelle jetzt erstmal laufen, bis die (gleichverteilte) Anfangspopulation weitgehend ausgestorben ist (nämlich N ⋅ L Runden) und ziehe dann nochmal für N ⋅ L Runden Statistiken, vor allem die mittlere Schurkigkeit in Abhängigkeit von der Hierarchieebene. Die kann ich dann übereinanderplotten, wobei ich die Zeit durch den Grauwert einfließen lasse (spätere, wahrscheinlich etwas relaxiertere, Zustände sind dunkler):

    Dabei ist auf der Abszisse die mittlere Hierarchieebene, auf der Ordinate die mittlere Schurkigkeit auf der entsprechenden Ebene; die Zeit ist, wie gesagt, durch den Grauwert der Punkte angedeutet und sorgt für die Streuung.

    Am auffälligsten ist wohl, dass Schurkigkeit auf den letzten paar Stufen am drastischsten ansteigt. Das hätte ich in dem Ausmaß nicht erwartet und deckt sich jedenfalls nach meiner Erfahrung nicht mit irgendwelchen Realitäten (in denen die Schurkigkeit schon auf nur moderat schwindelerregenden Ebenen rapide wächst). Ich komme gegen Ende nochmal etwas quantitativer auf die Steilheit des Anstiegs zurück.

    Hier, wie auch sonst, sind die Modelle bezeichnet durch einen String – sunde2.py verwendet ihn als Dateinamen –, der aus einer Bezeichnung der Verteilung (hier Exponential mit λ=4), der Zahl der Level N, dem Schurken-Vorteil und dem Lebenszeit-Faktor L besteht.

    Eine andere Art, diese Daten anzusehen, die insbesondere etwas mehr von der Dynamik erahnen lässt, ist eine Heatmap der Schurkigkeit; hier laufen die Hierarchieebenen auf der Ordinate, die Zeit auf der Abszisse; aus Bequemlichkeitsgründen hat hier die höchste Ebene mal die Bezeichnung 0 (so ist das übrigens auch im Programm gemacht, in den anderen Grafiken ist dagegen Ebene 50 das Nüßlein-Territorium):

    In-joke: Regenbogen-Palette. Ich habe gerade frei, ich darf das.

    Hier lässt sich ganz gut erkennen, dass der Kram nach einer maximalen Lebensdauer (da fängt die Grafik an) weitgehend relaxiert ist, und wieder, dass die letzten paar Hierarchieebenen die dramatischsten Schurken-Konzentrationen aufweisen. Die schrägen Strukturen, die überall sichtbar sind, sind zufällige Schurken-Konzentrationen auf der Karriereleiter. Intuitiv wäre wohl zu erwarten, dass sich Engel in Haifischbecken eher noch schwerer tun und so Schurkigkeitszonen selbstverstärkend sein könnten. Insofern ist die relativ geringe Streifigkeit der Grafik – die sagt, dass das wenigstens im Modell nicht so ist – erstmal eher beruhigend.

    Umgekehrt bilde mich mir ein, dass im unteren Bereich der Grafik einige blauere (also: engeligere) Strukturen deutlich flacher als 45 Grad laufen: Das könnten Engel-Konzentrationen sein, die gemeinsam langsamer die Karriereleiter besteigen. Fänd ich putzig (wenns die Karriereleiter denn schon gibt), kann aber auch nur überinterpretiertes Rauschen sein.

    Und noch eine Auswertung von diesem spezifischen Modell: Alter über Hierarchieebene, was angesichts des aktuellen Alte-weiße-Männer-Diskurses vielleicht interessant sein mag:

    Diese Abbildung funktioniert so wie die der mittleren Schurkigkeit, nur ist auf der Ordinate jetzt das Alter statt der Schurkigkeit. In dem Modell leben Aktoren ja zwei Mal die Zahl der Hierarchieebenen Runden, hier also 100 Runden. Die Aktoren ganz unten sind erkennbar deutlich jünger als der Schnitt (der bei 50 liegt), ganz oben sammeln sich alte Aktoren. Klingt speziell in dieser Ausprägung, in der oben wirklich nur Aktoren kurz vom Exitus sind, irgendwie nach später Sowjetunion, und klar ist das Modell viel zu einfach, um etwas wie die City of London zu erklären.

    Note to self: Beim nächsten Mal sollte ich mal sehen, wie sich das mittlere Alter von Schuken und Engeln in den unteren Schichten so verhält.

    Mal systematisch

    Weil Simulationen dieser Art schrecklich viele Parameter haben, ist das eigentlich Interessante, den Einfluss der Parameter auf die Ergebnisse zu untersuchen. Dazu habe ich mir mal ein paar Modelle herausgesucht, die verschiedene Parameter variieren (in der run_many-Funktion von sunde2); Ausgangspunkt sind dabei 50 Ebenen mit einem Lebenszeit-Faktor von zwei und einem Schurkenvorteil von 0.66. Das kombiniere ich mit:

    • einer Gleichverteilung von Schurkigkeiten
    • einer Exponentialverteilung mit λ = 2
    • einer Exponentialverteilung mit λ = 4
    • einer Exponentialverteilung mit λ = 4, aber einem Schurkenvorteil von 0.75
    • einer Exponentialverteilung mit λ = 4, aber einem Lebenszeit-Faktor von 4
    • einer Normalverteilung um 0.75 …

  • Fast alles Schurken

    12021:057:1 ( 2021-02-26)

    Die gerade durch die Medien gehende Geschichte von Georg Nüßlein zeichnet, ganz egal, was an Steuerhinterziehung und Bestechung nachher übrig bleibt, jedenfalls das Bild von einem Menschen, der, während rundrum die Kacke am Dampfen ist, erstmal überlegt, wie er da noch den einen oder anderen Euro aus öffentlichen Kassen in seine Taschen wandern lassen kann.

    Die Unverfrorenheit mag verwundern, nicht aber, dass Schurken in die Fraktionsleitung der CSU aufsteigen. Im Gegenteil – seit ich gelegentlich mal mit wichtigen Leuten umgehe, fasziniert mich die Systematik, mit der die mittlere Schurkigkeit von Menschen mit ihrer Stellung in der Hierarchie steil zunimmt: Wo in meiner unmittelbaren Arbeitsumgebung eigentlich die meisten Leute recht nett sind, gibt es unter den Profen schon deutlich weniger Leute mit erkennbarem Herz. Im Rektorat wird es schon richtig eng, und im Wissenschaftsministerium verhalten sich oberhalb der Sekretariate eigentlich alle wie Schurken, egal ob nun früher unter Frankenberg oder jetzt unter Bauer.

    Tatsächlich ist das mehr oder minder zwangsläufig so in Systemen, die nach Wettbewerb befördern. Alles, was es für ein qualitatives Verständnis dieses Umstands braucht, sind zwei Annahmen, die vielleicht etwas holzschnittartig, aber, so würde ich behaupten, schwer zu bestreiten sind.

    1. Es gibt Schurken und Engel
    2. Wenn Schurken gegen Engel kämpfen (na ja, wettbewerben halt), haben die Schurken in der Regel bessere Chancen.

    Die zweite Annahme mag nach dem Konsum hinreichend vieler Hollywood-Filme kontrafaktisch wirken, aber eine gewisse moralische Flexibilität und die Bereitschaft, die Feinde (na ja, Wettbewerber halt) zu tunken und ihnen auch mal ein Bein zu stellen, dürfte unbestreitbar beim Gewinnen helfen.

    Um mal ein Gefühl dafür zu kriegen, was das bedeutet: nehmen wir an, der Vorteil für die Schurken würde sich so auswirken, dass pro Hierarchieebene der Schurkenanteil um 20% steigt, und wir fangen mit 90% Engeln an (das kommt für mein soziales Umfeld schon so in etwa hin, wenn mensch hinreichend großzügig mit dem Engelbegriff umgeht). Als Nerd fange ich beim Zählen mit Null an, das ist also die Ebene 0.

    Auf Ebene 1 sind damit noch 0.9⋅0.8, also 72% der Leute Engel, auf Ebene 2 0.9⋅0.8⋅0.8, als knapp 58% und so fort, in Summe also 0.9⋅0.8n auf Ebene n. Mit diesen Zahlen sind in Hierarchieebene 20 nur noch 1% der Leute Engel, und dieser Befund ist qualitativ robust gegenüber glaubhaften Änderungen in den Anfangszahlen der Engel oder der Vorteile für Schurken.

    Tatsächlich ist das Modell schon mathematisch grob vereinfacht, etwa weil die Chancen für Engel sinken, je mehr Schurken es gibt, ihr Anteil also schneller sinken sollte als hier abgeschätzt. Umgekehrt sind natürlich auch Leute wie Herr Nüßlein nicht immer nur Schurken, sondern haben manchmal (wettbewerbstechnisch) schwache Stunden und verhalten sich wie Engel. Auch Engel ergeben sich dann und wann dem Sachzwang und sind von außen von Schurken nicht zu unterscheiden. Schließlich ist wohl einzuräumen, dass wir alle eher so eine Mischung von Engeln und Schurken sind – wobei das Mischungsverhältnis individuell ganz offensichtlich stark schwankt.

    Eine Simulation

    All das in geschlossene mathematische Ausdrücke zu gießen, ist ein größeres Projekt. Als Computersimulation jedoch sind es nur ein paar Zeilen, und die würde ich hier gerne zur allgemeinen Unterhaltung und Kritik veröffentlichen (und ja, auch die sind unter CC-0).

    Ein Ergebnis vorneweg: in einem aus meiner Sicht recht plausiblen Modell verhält sich die Schurkigkeit (auf der Ordinate; 1 bedeutet, dass alle Leute sich immer wie Schurken verhalten) über der Hierarchiebene (auf der Abszisse, höhere Ebenen rechts) wie folgt (da sind jeweils mehrere Punkte pro Ebene, weil ich das öfter habe laufen lassen):

    Graph: Scatterplot von Schurkigkeit gegen Karriereschritt

    Ergebnis eines Laufs mit einem Schurken-Vorteil von 0.66, mittlere Schurkigkeit über der Hierarchieebene: Im mittleren Management ist demnach zur 75% mit schurkigem Verhalten zu rechnen. Nochmal ein paar Stufen drüber kanns auch mal besser sein. Die große Streuung auf den hohen Hierarchieebenen kommt aus den kleinen Zahlen, die es da noch gibt; in meinen Testläufen fange ich mit 220 (also ungefähr einer Million) Personen an und lasse die 16 Mal Karriere machen; mithin bleiben am Schluss 16 Oberchefs übrig, und da macht ein_e einzige_r Meistens-Engel schon ziemlich was aus.

    Das Programm, das das macht, habe ich Schurken und Engel getauft, sunde.py – und lade zu Experimenten damit ein.

    Zunächst das Grundmodell, in Python formuliert:

    ROGUE_ADVANTAGE = 0.66

_WIN_PROB = {
    (False, False): 0.5,
    (False, True): 1-ROGUE_ADVANTAGE,
    (True, False): ROGUE_ADVANTAGE,
    (True, True): 0.5,}

class Actor:
    def __init__(self, angelicity):
        self.angelicity = angelicity

    def is_rogue(self):
        return random.random()>self.angelicity

    def wins_against(self, other):
        return _WIN_PROB[self.is_rogue(), other.is_rogue()]>random.random()

    Es wird also festgelegt, dass, wenn ein Schurke gegen einen Engel wettbewerbt, der Schurke mit zu 66% gewinnt (und ich sage mal voraus, dass der konkrete Wert hier qualitativ nicht viel ändern wird), während es ansonsten 50/50 ausgeht. Das ist letztlich das, was in _WIN_PROB steht.

    Und dann gibt es das Menschenmodell: Die Person wird, wir befinden uns in gefährlicher Nähe zu Wirtschafts„wissenschaften“, durch einen Parameter bestimmt, nämlich die Engeligkeit (angelicity; das Wort gibts wirklich, meint aber eigentlich nicht wie hier irgendwas wie Unbestechlichkeit). Diese ist die Wahrscheinlichkeit, sich anständig zu verhalten, so, wie das in der is_rogue-Methode gemacht ist: Wenn eine Zufallszahl zwischen 0 und 1 (das Ergebnis von random.random()) großer als die Engeligkeit ist, ist die Person gerade schurkig.

    Das wird dann in der wins_against-Methode verwendet: sie bekommt eine weitere Actor-Instanz, fragt diese, ob sie gerade ein Schurke ist, fragt sich das auch selbst, und schaut dann in _WIN_PROB nach, was das für die Gewinnwahrscheinlichkeit bedeutet. Wieder wird das gegen random.random() verglichen, und das Ergebnis ist, ob self gegen other gewonnen hat.

    Der nächste Schritt ist die Kohorte; die Vorstellung ist mal so ganz in etwa, dass wir einem Abschlussjahrgang bei der Karriere folgen. Für jede Ebene gibt es eine Aufstiegsprüfung, und wer die verliert, fliegt aus dem Spiel. Ja, das ist harscher als die Realität, aber nicht arg viel. Mensch fängt mit vielen Leuten an, und je weiter es in Chef- oder Ministerialetage geht, desto dünner wird die Luft – oder eher, desto kleiner die actor-Menge:

    class Cohort:
    draw = random.random

    def __init__(self, init_size):
        self.actors = set(Actor(self.draw())
            for _ in range(init_size))

    def run_competition(self):
        new_actors = set()
        for a1, a2 in self.iter_pairs():
            if a1.wins_against(a2):
                new_actors.add(a1)
            else:
                new_actors.add(a2)

        self.actors = new_actors

    def get_meanness(self):
        return 1-sum(a.angelicity
          for a in self.actors)/len(self.actors)

    (ich habe eine technische Methode rausgenommen; für den vollen Code vgl. oben).

    Interessant hier ist vor allem das draw-Attribut: Das zieht nämlich Engeligkeiten. In dieser Basisfassung kommen die einfach aus einer Gleichverteilung zwischen 0 und 1, wozu unten noch mehr zu sagen sein wird. run_competition ist der Karriereschritt wie eben beschrieben, und get_meanness gibt die mittlere Schurkigkeit als eins minus der gemittelten Engeligkeit zurück. Diesem Wortspiel konnte ich nicht widerstehen.

    Es gäbe zusätzlich zu meanness noch interessante weitere Metriken, um auszudrücken, wie schlimm das Schurkenproblem jeweils ist, zum Beispiel: Wie groß ist der Anteil der Leute mit Engeligkeit unter 0.5 in der aktuellen Kohorte? Welcher Anteil von Friedrichs (Engeligkeit<0.1) ist übrig, welcher Anteil von Christas (Engeligkeit>0.9)? Aus wie vielen der 10% schurkgisten Personen „wird was“? Aus wie vielen der 10% Engeligsten? Der_die Leser_in ahnt schon, ich wünschte, ich würde noch Programmierkurse für Anfänger_innen geben: das wären lauter nette kleine Hausaufgaben. Andererseits sollte mensch wahrscheinlich gerade in so einem pädagogischen Kontext nicht suggerieren, dieser ganze Metrik-Quatsch sei unbestritten. Hm.

    Nun: Wer sunde.py laufen lässt, bekommt Paare von Zahlen ausgegeben, die jeweils Hierarchiestufe und meanness der Kohorte angeben. Die kann mensch dann in einer Datei sammeln, etwa so:

    $ python3 sunde.py >> results.txt
$ python3 sunde.py >> results.txt

    und so fort. Und das Ganze lässt sich ganz oldschool mit gnuplot darstellen (das hat die Abbildung oben gemacht), z.B. durch:

    plot "results.txt" with dots notitle

    auf der gnuplot-Kommandozeile.

    Wenn mir wer ein ipython-Notebook schickt, das etwa durch matplotlib plottet, veröffentliche ich das gerne an dieser Stelle – aber ich persönlich finde shell und vi einfach eine viel angenehmere Umgebung...

    Anfangsverteilungen

    Eine spannende Spielmöglichkeit ist, die Gesellschaft anders zu modellieren, etwa durch eine Gaußverteilung der Engeligkeit, bei der die meisten Leute so zu 50% halb Engel und halb Schurken sind (notabene deckt sich das nicht mit meiner persönlichen Erfahrung, aber probieren kann mensch es ja mal).

    Dazu ersetze ich die draw-Zuweisung in Cohort durch:

    def draw(self):
     return min(1,
         max(0, random.normalvariate(0.5, 0.25)))

    Die „zwei Sigma“, also – eine der wichtigeren Faustformeln, die mensch im Kopf haben sollte – 95% der Fälle, liegen hier zwischen 0 und 1. Was drüber und drunter rausguckt, wird auf „immer Engel“ oder „immer Schurke“ abgeschnitten. Es gibt in diesem Modell also immerhin 2.5% Vollzeitschurken. Überraschenderweise sammeln sich die in den ersten 16 Wettbewerben nicht sehr drastisch in den hohen Chargen, eher im Gegenteil:

    Graph: Scatterplot wie oben, nur für gaussverteilte Aktoren

    Deutlich plausibler als die Normalverteilung finde ich in diesem Fall ja eine …

  • Solidarität ist... charmant

    12021:053:1 ( 2021-02-22)
    Ein Weißbüschelaffe

    Sucht nach netten Genoss_innen: ein Weißbüschelaffe – Raimond Spekking / CC BY-SA 4.0 (via Wikimedia Commons)

    An sich halte ich ja Soziobiologie für irgendwas zwischen Mumpitz und reaktionärer Zumutung, jedenfalls soweit sie verstanden wird als Versuch, menschliches Verhalten oder gar gesellschaftliche Verhältnisse durch biologische Befunde (oder das, was die jeweiligen Autor_innen dafür halten) zu erklären und in der Folge zu rechtfertigen.

    Hier ist aber eine Geschichte (DOI 10.1126/sciadv.abc8790), die so putzig ist, dass ich mir in der Beziehung etwas mehr Toleranz von mir wünschen würde. Und zwar hat eine Gruppe von Anthropolog_innen um Rahel Brügger aus Zürich das Kommunikationsverhalten von Weißbüschelaffen untersucht (Disclaimer: Nee, ich finde eigentlich nicht, dass mensch Affen in Gefangenschaft halten darf, aber in diesem Fall scheint zumindest das expermimentelle Protokoll halbwegs vertretbar).

    Dabei haben sie zunächst zwei Dialoge zwischen (den Proband_innen unbekannten) Affen aufgenommen: Ein Affenkind hat einen erwachsenen Affen um Futter angebettelt. Im einen Fall hat der erwachsene Affe abgelehnt, im anderen Fall wohl etwas wie „schon recht“ gemurmelt.

    Dann haben sie die Aufnahmen anderen Affen vorgespielt und haben dann geschaut, ob diese lieber weggehen oder lieber nachsehen, wer da geplaudert hat. Und siehe da: Die Tiere wollten viel lieber die netten Affen sehen als die doofen. Bei den netten Affen haben nach gut 10 Sekunden schon die Hälfte der Proband_innen nachgesehen, wer das wohl war, bei den doofen war das mehr so 30 Sekunden. Und bis zum Ende der jeweiligen Versuche nach zwei Minuten wollten immerhin ein Viertel der Proband_innen nichts von den doofen Affen sehen, aben nur ein Zehntel nichts von den netten.

    Moral: Seid nett, und die Leute mögen euch.

    Ja, ok, kann sein, dass die Äffchen nur gehofft haben, dass sie auch Essen kriegen, wenn schon das Kind was bekommen hat. Pfft. Ich sag ja, Soziobiologie stinkt.

    Nachbemerkung 1: Ich habe das auch nicht gleich in Science Advances gefunden (da gäbs andere Journals, die ich im Auge haben sollte), sondern in den Meldungen vom 4.2. des sehr empfehlenswerten Forschung aktuell im Deutschlandfunk.

    Nachbemerkung 2: Ich weiß, Literatur soll mensch nicht erklären, aber die Überschrift ist natürlich ein Einwand gegen einen der Wahlsprüche der Roten Hilfe: „Solidarität ist eine Waffe“. So klasse ich die Rote Hilfe finde, der entschlossene Pazifist in mir hat die Parole nie so recht gemocht. Mensch will ja eigentlich weniger Waffen haben, aber ganz bestimmt mehr Solidarität.

  • Das letzte Bild

    12021:035:1 ( 2021-02-04)
    Pale Blue Dot, hochgezoomt

    Das Pale Blue Dot-Bild, mit Gimps Lens Distortion ordentlich verhackstückt, damit es auch wirklich blassblau wird.

    In meinem asynchronen Radio habe ich heute Voyager 3 gehört, ein Feature über... na ja, alles mögliche, insbesondere aber die kulturellen Implikationen der Golden Records an Bord der Voyagers. Streckenweise wars großartig; manchmal sind diese freistil-Features ja offensiv langweilig, aber dann lassen mich solche Highlights doch immer an meiner (na ja, der meines Computers) Mitschneideroutine am Sonntagabend festhalten.

    In dieser Sendung gab es erstmal ein paar Genau-mein-Humor-Witze zu den Platten, etwa:

    Warum ist da nicht mehr Bach drauf? – Wir wollten nicht so angeben.

    Gefakte Durchsage der (vielleicht der NASA): Es ist nicht viel, aber es ist die erste Nachricht einer fremden Zivilisation. Vier Worte: Send more Chuck Berry.

    Natürlich sind die Golden Records selbst schon zutiefst anrührend und romatisch. Aber dann kam gegen Ende der Sendung noch etwas, das ich, nennt mich einen irren Nerd, besonders anrührend fand. Sie haben nämlich die Geschichte vom Pale Blue Dot (PBD) erzählt, nach dem Voyager 1, bevor die Kamera endgültig abgeschaltet wurde, umgedreht wurde und aus gut 40 Astronmischen Einheiten Entfernung die Erde portraitiert hat.

    Diese Geschichte kannte ich als Carl-Sagan-Fan natürlich schon, aber in dieser Darstellung klang es so, als sei der PBD das letzte Bild der Kamera gewesen, und dabei kam mir der ergreifende Gedanke: oh wow, da haben sie das Bild der Erde sozusagen in die Netzhaut der sterbenden Kamera (ihr Band) eingebrannt, und wenn dann dermaleinst Aliens die Sonde bergen, würden sie das eben diese Erinnerung an die Ursprungswelt dort noch finden.

    Leider ist das natürlich alles Quatsch. Erstens war das PBD-Bild gar nicht das letzte, das die Kamera geschossen hat, schon, weil die Kamera (wie eigentlich immer noch alle wissenschaftlichen Kameras in der Astronomie) monochrom war und es drum schon mal drei Aufnahmen gewesen wäre, aber auch, weil Voyager als Teil der Rückschau einen ganzen Haufen anderer Aufnahmen machte und so zuletzt vielleicht die Sonne oder Neptun angeschaut hat, aber nicht die Erde.

    Aber selbst wenn die Erd-Bilder die letzten gewesen wären, wären sie wahrscheinlich nicht auf dem Bandlaufwerk geblieben, denn die Voyagers nehmen ja immer noch Daten, und ich habe bis eben angenommen, dass die immer noch auf dem Bandlaufwerk zwischengespeichert werden. Allerdings berichtet hackaday, dass zumindest Voyager 1 inzwischen offenbar kein übers RAM funktioniert (beeindruckend, denn alle drei Rechner an Bord kommen zusammen gerade so über 64kB).

    Leider würde es auch nichts helfen, wenn es das PBD-Bild irgendwie geschafft hätte, trotz der weiteren Aktivitäen von Voyager 1 auf dem Band zu bleiben: Selbst bei den tiefen Temperaturen dort draußen wird die Magnetisierung des Bandes allein schon wegen der kosmischen Strahlung bald verschwunden sein. Die Aliens werden eben leider doch nicht die Erde als letztes Bild der sterbenden Kamera verewigt sehen. Schade.

    Ach übrigens: Voyager 1 steht übrigens gerade im Schlangenträger. Ganz einsam. Was auch eine gewisse Romantik hat, denn im Schlangenträger steht auch der einsamste Stern am Himmel.

  • Klar: Corona

    12021:016:0 ( 2021-01-16)

    Ich kann nicht lügen: Einer der Gründe, weshalb ich gerade jetzt mit diesem Blog daherkomme ist, dass ich mir seit Dezember ganz besonders auf die Schulter klopfe wegen der Präzision meiner Corona-Vorhersagen: Wie befriedigend wäre es gewesen, wenn ich auf was Öffentliches hinweisen könnte, das meine Vorhersagen Anfang November dokumentieren würde. Als der „weiche Lockdown“ losging, habe ich nämlich etwas verkniffen rumerzählt: Klar werden die Zahlen nicht runtergehen, solange die Betriebe [1] nicht massiv runterfahren, und weil sich das niemand traut, werden in der Folge immer bizarrere Maßnahmen getroffen werden.

    So ist es nun gekommen, bis hin zu den Windmühlenkämpfen gegen die Rodler_innen im Sauerland und die nächtlichen Ausgangssperren hier in Baden-Württemberg (die allerdings, soweit ich das erkennen kann, genau niemand durchsetzt).

    Nun, jetzt habe ich die nächste Gelegenheit. Zu den relativ wenig beachteten Phänomenen gerade gehört nämlich, dass die Zahl der Corona-Intensivpatient_innen seit dem 4.1. konsistent fällt. Ich bin ziemlich überzeugt, dass das im Wesentlichen das Runterfahren von eigentlich praktisch allem (Betriebe, Geschäfte, Schulen) in der Woche vor Weihnachten spiegelt; und das würde auch darauf hinweisen, dass die Intensivbelegung dem Infektionsgeschehen etwas weniger als die generell angenommenen drei Wochen hinterherläuft.

    Tatsächlich lasse ich seit September jeden Tag ein ad-hoc-Skript laufen, das die aktuellen DIVI-Zahlen aus dem RKI-Bericht des Tages extrahiert und dann logarithmisch (also: exponentielle Entwicklung ist eine Gerade) plottet. Das sieht dann etwa so aus:

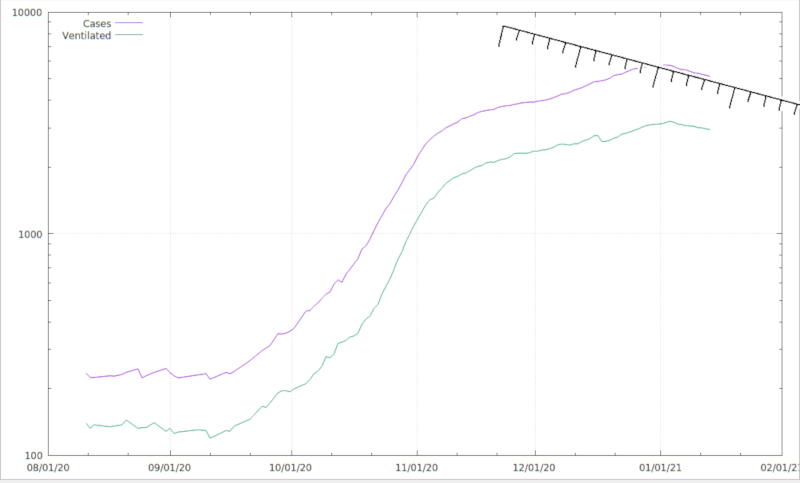
    Plot: Intensivbelegung 9/2020-1/2021

    Das angebrachte Lineal ist ein kleiner Python-Hack, den ich extra dafür gemacht habe (da schreibe ich bestimmt demnächst auch mal was zu), und er zeigt: Wir haben seit fast zwei Wochen einen exponentiellen Rückgang der Intensivbelegung – auch bei den Beatmeten, was die untere Linie zeigt; deren paralleler Verlauf lässt übrigens ziemlich zuverlässig darauf schließen, dass wohl keine im Hinblick auf den Verlauf aggressivere Mutante in großer Zahl unterwegs ist.

    Die schlechte Nachricht: Wenn mensch die Steigung anschaut, kommt eine Halbierungszeit von was wie sechs Wochen raus. Das wird nicht reichen, zumal, und hier kommt jetzt meine Prognose, diese Entwicklung wohl bald gebrochen wird, denn zumindest in meiner Umgebung war die Weihnachtsruhe spätestens am 11.1. vorbei, in Bundesländern ohne Feiertag am 6. wahrscheinlich schon früher. Unter der Annahme von zweieinhalb Wochen zwischen Infektionsgeschehen und Intensivreaktion dürfte es dann also etwa Mitte nächster Woche so oder so vorbei sein mit dem Traum zurückgehender Infektionen.

    Und wenn ich schon über Coronazahlen rede: Diesen Belegungsplot mache ich, weil ich ziemlich sicher bin, dass von all den Zahlen, die das RKI derzeit verbreitet, nur die DIVI-Zahlen überhaupt ziemlich nah an dem sind, was sie zu sagen vorgeben, auch wenn Peter Antes, auf dessen Urteil ich viel gebe, da neulich auch Zweifel geäußert hat, die ich erstmal nicht ganz verstehe: die zwei „komischen“ Schnackler, die ich sehe, sind jetzt mal wirklich harmlos.

    Dass die Infektionszahlen problematisch sind, ist inzwischen ein Gemeinplatz; zwar wäre sicher, könnte mensch wirklich den Zeitpunkt der Übertragung in nennenswerter Zahl feststellen, ein sichtbarer Effekt vom Wochenende zu sehen (denn die Übertragung in der Breite dürfte derzeit stark von Arbeit und Arbeitsweg dominiert sein), aber nicht mal der würde die wilden Zacken verursachen, an die wir uns in den letzten Monaten gewöhnt haben.

    Aber ok – dass in Daten dieser Art das Wochenende sichtbar ist, hätte ich auch bei 24/7-Gesundheitsämtern jederzeit vorhergesagt. Beim besten Willen nicht vorhergesagt hätte ich allerdings die Zackigkeit dieser Kurve:

    Plot: Corona-Tote über Tag von JHU

    Zu sehen sind hier die Todesmeldungen pro Tag (jetzt nicht vom RKI, sondern von Johns Hopkins, aber beim RKI sieht das nicht anders aus). Sowohl nach Film-Klischee („Zeitpunkt des Todes: Dreizehnter Erster, Zwölf Uhr Dreiunddreissig“) als auch nach meiner eigenen Erfahrung als Zivi auf einer Intensivstation hätte ich mir gedacht, dass Sterbedaten im Regelfall zuverlässig sind. Und so sehr klar ist, dass während Volksfesten mehr Leute sterben und bei den Motorradtoten ein deutliches Wochenend-Signal zu sehen sein sollte: Corona kennt ganz sicher kein Wochenende.

    Also: DIVI rules.

    Und ich muss demnächst wirklich mal gegen dark mode ranten.

    [1]Als bekennender Autofeind muss ich ja zugeben, dass der größte Wow-Effekt der ganzen Corona-Geschichte war, als im letzten März VW die Produktion eingestellt hat. Dass ich das noch erleben durfte... Der zweitgrößte Wow-Effekt war übrigens, dass die doch ziemlich spürbare Reduktion im Autoverkehr im März und April sich nicht rasch in den Sterblichkeitsziffern reflektiert hat.

« Seite 3 / 3

Letzte Ergänzungen