Engelszüngeln Home

Abenteuer Irland: Kaputtes Drupal und eine Mail an die Datenschutzbehörde

12022:242:1 ( 2022-08-30)
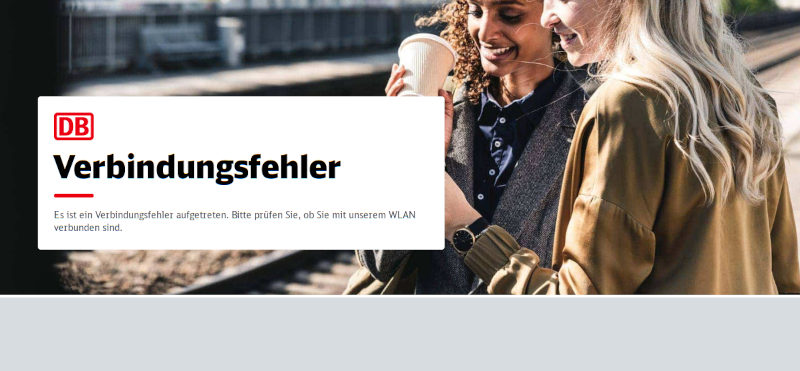
Als Reaktion auf meinen Hilferuf gegen Google hat @ulif@chaos.social getrötet:

Vielleicht einfach mal unverbindlich bei der irischen "Datenschutzbehörde" nachfragen? Nicht als Beschwerde, sondern als einfache Anfrage. Denen müssen sie diese Daten ja eigentlich gemeldet haben.

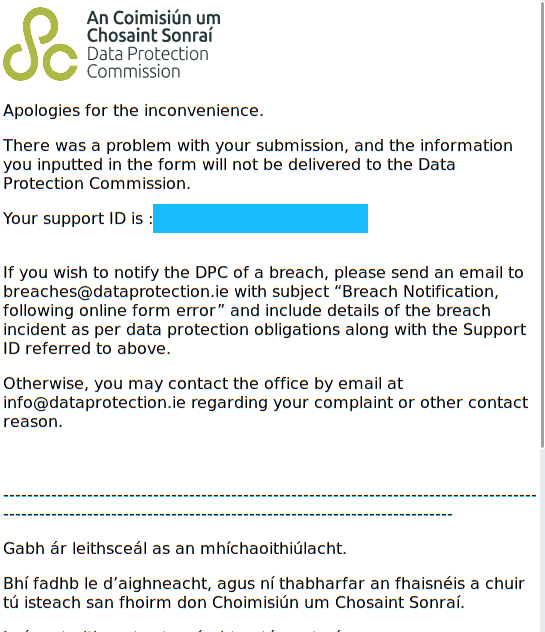
Na schön. Das könnte interessant werden. Das erste Ergebnis einer duckduckgo-Anfrage nach „data protection ireland“. führt gleich zur data protection commission (bzw. Choimisiún um Chosaint Sonraí), https://www.dataprotection.ie/, und ich bekomme beim Draufklicken original das hier:

Keine GET-Parameter, kein POST-Payload, einfach nur https://www.dataprotection.ie/, und schon habe ich eine support ID. Oh wow. Interessanterweise ändert sich das auch nicht, wenn ich dataprotection.ie Javascript erlaube; mit einem Firefox (statt einem luakit) erscheint hingegen die Webseite, wie sich die Leute das wohl vorgestellt haben.

Wie kommt das? Ich curl-e mal eben die Seite und sehe schon recht weit oben:
```
<meta name="twitter:card" content="summary_large_image" />
<meta name="twitter:site" content="@dpcireland" />
<meta name="twitter:title" content="Homepage | Data Protection Commission" />
```
und noch ein paar mehr Zeilen Twitter-Service. Diese Leute sollten dringend mal ihrem Kollegen in Baden-Württemberg zuhören.

Immerhin kommen aber keine Webfonts von Google, und es laufen auf den ersten Blick auch keine externen Tracking-Dienste („Analytics“). Aber ich finde kein Refresh-Meta oder etwas anderes, das erklären könnte, warum luakit diese eigenartige Fehlermeldung ausgeliefert bekommen könnte, während an curl und firefox recht anständige Antworten gehen.

Leider macht auch dataprotection.ie die bedauerlichen Zwangs-Redirects auf https, so dass es nicht ganz einfach ist, zuzusehen, was mein Browser und der Webserver der IrInnen eigentlich miteinander ausmachen. Aber ich bin neugierig genug auf das, was da zwischen meinem Browser und dem dataprotection.ie-Server vorgeht, dass ich meinen mitmproxy auspacke und damit in die Kommunikation meines eigenen Computers einbreche[1].

Auf diese Weise sehe ich meinen Request:
```
GET https://www.dataprotection.ie/
Host: www.dataprotection.ie
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,*/*;q=0.8
User-Agent: Tracking is lame.
Accept-Encoding: gzip, deflate
Accept-Language: C
Connection: Keep-Alive
```
Ah… richtig… ich bin ein wenig gemein mit der Sprach-Aushandlung in meinem normalen Browser und frage die Webseiten nach der Sprache C (was weniger gemein ist als es scheinen mag, aber das ist ein längeres Thema). Ein schnelles Experiment bestätitgt, dass es das ist, was den Drupal (das ist das Programm, das deren Webseite macht) der irischen Datenschutzbehörde getötet hat.

Wenn das noch oder wieder kaputt ist[2], wenn du das hier liest, ist eine einfache Kommandozeile, um das Problem zu reproduzieren:
```
$ curl -s -H "Accept-Language: C" https://www.dataprotection.ie/ | head -5
<!DOCTYPE html>
<html lang="en">
<head>
<title> Website error notice | Data Protection Commission </title>
</head>
```
Aber egal, ich war ja eigentlich nicht hier, um Webseiten zu debuggen. Wichtig ist: Ich habe eine Mailadresse. Und das ist viel besser als das, was auf der normalen Webseite steht:

Echt jetzt? Papierpost ist ja schon noch sowas wie ein offener Standard, aber dann nur die proprietären, überwachungskapitalistischen Dienste Twitter, Instagram und Linkedin für Kontaktaufnahme anzubieten und nicht die offene Mail, das wäre auch für einen normalen Laden schon ein starkes Stück. Für eine Datenschutzbehörde… Na ja, ok, wir reden hier über die irische.

Immerhin steht in deren data protection statement:

If you wish to contact our Data Protection Officer in relation to the processing of your personal data by the Commission, you can do so by e-mailing dpo@dataprotection.ie.

Schön: immerhin gibts da eine Mailadresse, bei der ich mich beschweren könnte, aber ganz ehrlich: Anständige DatenschützerInnen sollten da bitte noch einen PGP-Schlüssel dazuschreiben. Jaja, ich weiß: das hier sind die irischen…

Ich sollte natürlich nicht so voreingenommen sein; nur weil die bisher ein Witz waren, heißt das ja nicht, dass sie das auch weiter sein werden, und so habe ich ihnen gerade eine Mail geschickt:

Dear DPO,

It seems your staff has already fixed it, presumably after I triggered some sort of alarm system while investigating the problem (in which case: apologies!), but your CMS until a few minutes ago produced error messages like the one on http://blog.tfiu.de/media/2022/ie-data-protection-breakage.png when queried with an

Accept-Language: C

header. I'm reporting this partly to make sure the apparent fix wasn't a fluke. If it wasn't: kudos to your operations people to have noticed and fixed the problem so quickly.

While I'm here, can I also put forward the reason I'm contacting you in the first place?

You see, I'm trying to get rid of a Google account I created perhaps 15 years ago. To do that, Google tells me to log in. When I try that, Google asks for the e-mail address associated to the account (which is <withheld here>), then for the password. After I've put that in, Google sends a mail to the account with a confirmation code, which is perhaps not entirely unreasonable given I've steered clear of Google services requiring authentication for many years.

But even after entering that confirmation code, it will not let me in, requiring me to enter a telephone number. This is absolutely unreasonable, and I would be grateful if you could tell Google that much; given that Google does not know any telephone number associated to me, there is no way this information could fend off abuse. This is clearly a blantant attempt to skim off the extra piece of data.

I would normally not be bothering you with this obvious imposition, though; I would have liked to first take this to Google's data protection officer. However, I was unable to locate contact information in Google's privacy statements (I was served the German version), which I claim is in open violation of GDPR Article 13. So, could you

(a) tell Google to publish a proper e-mail contact address as part of their GDPR information? While I have to admit that the GDPR is not explicit about it, it is clear to me that Google's own web forms, in particular when they require Javascript and Captchas, or, even worse, a google id, are insufficient to fulfil Art 13 1 (b) GDPR.

(b) meanwhile, provide me with the contact e-mail of Google's data protection officer so I can take my issue to them myself?

Thanks,

(not Anselm Flügel)

Ich bin neugierig, wie es weitergeht. Lobend will ich schon mal erwähnen, dass der irische DPO offenbar keine automatisierten Empfangsbestätigungen („Wir werden uns Ihrem Anliegen so bald wie möglich widmen“) verschickt.

Fortsetzung folgt. Voraussichtlich.

Nachtrag (2022-08-31)

Ich muss das Lob zurücknehmen. Es gab doch eine (halb-) automatisierte Empfangsbestätigung, abgeschickt um 14:47 Lokalzeit in Dublin. Für ein Verfahren, das nur auf Computer setzt, ist das eine komische Zeit bei einer Mail, die am Vorabend um 19:17 MESZ rausging. Wirklich gelesen hat die Mail aber auch niemand. Das weiß ich schon, weil sie mich mit „To Whom It May Concern“ anreden, aber auch wegen der angesichts meiner Anfrage widersinnigen Empfehlung, ich möge mich doch an den Datenschutzbeauftragten „for that organisation“ wenden.

Weil Leute vielleicht später mal die Evolution des Kundendienstesisch des irischen DPO nachvollziehen wollen, belästige ich euch mit dem Volltext:

To Whom It May Concern,

I acknowledge receipt of your e-mail to the Data Protection Commission (DPC) .

In line with our Customer Service Charter, we aim to reply to the concerns raised by you within 20 working days, though complex complaints may require further time for initial assessment. In doing so, we will communicate clearly, providing you with relevant information or an update regarding your correspondence.

What can I do to progress my concern?

In the meantime, if your concern relates to processing of your personal data by an organisation (a “data controller”), or you wish to exercise your data protection rights (for example, access, erasure, rectification), you may wish to contact the data protection officer for that organisation in writing in the first instance. You may wish to forward copies of all written exchanges with the data controller to the DPC if you remain dissatisfied with the response you receive from them. You should send this documentation to info@dataprotection.ie and include the above reference number.

What if I have already contacted an organisation (“data controller”) about my concerns?

If you have already exchanged written correspondence with the data controller, and have not included this information with your initial contact with the DPC, you should send this documentation to info@dataprotection.ie quoting the case reference shown above.

What happens when I send the DPC additional correspondence or documents?

Please be advised that the Data Protection Commission does not issue acknowledgements for each item of follow up or supplementary correspondence received, but this correspondence will be included on the file reference above and assessed alongside your initial concern. Once this assessment has been carried out, a substantive response will be issued to you in due course.

This acknowledgement, and the reference number above, is confirmation that we have received your correspondence and that it will receive a response at the earliest opportunity.

Yours sincerely,

Alexandra X. [und noch ein Nachname]

[Ein paar Footer-Zeilen]

Is le haghaidh an duine nó an eintitis ar …
⎆
Google: Ohne Telefon kommst du hier nicht raus

12022:240:7 ( 2022-08-29)
Vor ungefähr 15 Jahren habe ich unvorsichtigerweise einen Google-Account angelegt – ich habe selbst vergessen, warum. Heute morgen hat mich Google an diese Jugendsünde (immerhin aus Zeiten, als Google noch nicht ganz so finster war) erinnert, weil sie eine Bestätigung haben wollten, dass die Mail-Adresse, die ich damals verwendet habe, noch existiert (tut sie).

Da ich an anmeldepflichtigen Google-Diensten genau gar kein Interesse habe, machte mich daran, den Account zu löschen. Und habe einen Haufen Zeit verschwendet, ohne irgendwohin zu kommen. Mit etwas Geduld habe ich zwar die leicht alarmistische Anleitung fürs Löschen bei Google gefunden. Dort heißt es nach viel Geschwätz:

Schritt 3: Konto löschen [auf einer Seite, die „Google-Konto löschen“ überschrieben ist, ist es ja schon tapfer, dass das Schritt 3 ist]

[...]

Gehen Sie in Ihrem Google-Konto zum Abschnitt Daten und Datenschutz.

Tja. Dafür müsste ich mich einloggen. Wenn ich das probiere, fordert Google zunächst einen per Mail versandten Bestätigungscode[1] und dann eine Telefonnummer, an die sie einen weiteren Bestätigungscode schicken wollen.

Das wäre auch dann frech, wenn ihnen die Telefonnummer irgendeine Hilfe wäre, unberechtigte Löschversuche zu unterbinden. Aber das ist sie hier nicht, denn alles, was Google von mir hat, ist diese Mailadresse, und dass ich über sie verfüge, habe ich bereits durch den ersten Bestätigungscode nachgewiesen. Soweit es mich betrifft, ist Googles Verhalten hier von Phishing nicht unterscheidbar.

Voll Zorn wäre ich nun gerne zum betrieblichen Datenschutzbeauftragten von Google gerannt; ich habe diese Woche noch nicht viel nichtssagendes Kundendienstesisch lesen müssen, und so denke ich, dass ich eine Antwort durchaus gleichmütig hätte ertragen können.

Aber nein, Artikel 13 DSGVO, nach der zu einer Datenschutzerklärung gehört:
1. gegebenenfalls die Kontaktdaten des Datenschutzbeauftragten,
gilt augenscheinlich nicht für Google. Beschweren müsste ich mich über diesen Gesetzesverstoß (und natürlich auch darüber, dass Google das Löschen meines Accounts effektiv verweigert) bei der Aufsichtsbehörde, und das ist die irische Datenschutzbehörde – ein Witz in zwei Wörtern.

Tja. Was tue ich jetzt? Ein Verwaltungsgerichtsverfahren ist mir ein seit Jahrzehnten toter Account auch nicht wert. Hat wer Ratschläge, wie ich diesen Google-Account trotzdem loswerde?

So oder so bleibt mein dringender Ratschlag an alle, die sich über Kaltschnäuzigkeit dieser Größenordnung noch ärgern können: Finger weg von Google!

[1] Schon das ist ja grenzwertig: Was ist denn, wenn ich die Mail-Adresse nicht mehr kontrolliere? Aber gut, das war jetzt nicht mein Problem.
⎆
Das BESTE Bildungssystem in Deutschland

12022:238:7 ( 2022-08-27)

Berlin Hauptbahnhof, August 2021: Würden Sie von Leuten, die Menschen an öffentlichen Orten mit solcher Werbung belästigen, Bildungsstudien kaufen?

In den DLF-Nachrichten vom 17.8. war in der 16:30-Ausgabe folgende Nachricht zu hören:

Sachsen hat laut einer aktuellen Erhebung das beste Bildungssystem in Deutschland. Das ergab eine Vergleichsstudie des Instituts der Deutschen Wirtschaft, das dieses [sic] im Auftrag der Initiative neue Soziale Marktwirtschaft erstellt [sic]. Bayern und Thüringen liegen auf den Plätzen zwei und drei. Schlusslicht ist hinter Nordrhein-Westfalen und Sachsen-Anhalt der Stadtstaat Bremen.

Als ich eben einen Mitschnitt davon beim Radfahren gehört habe, musste ich in aller Öffentlichkeit hysterisch lachen. In Momenten wie diesen bin ich froh, dass die Gesellschaft längst an unpassende Interaktionen zwischen Menschen und ihren technischen Gerätschaften, auch und gerade mitten auf der Straße, gewöhnt ist.

Sowohl das zugrundeliegende Ereignis als auch das Framing durch die DLF-Redaktion werfen mal wieder die Frage auf, was Satire eigentlich alles darf. Lieber DLF, was wäre verkehrt gewesen an neutraler Berichterstattung, sagen wir:

Die Abteilung INSM der Werbeagentur Scholz & Friends versucht, mit der Behauptung, ausgerechnet das immer wieder durch die Prävalenz sehr eigenartiger Ansichten auffällige Sachsen habe das – im Sinne von der INSM geeignet definierter Kriterien – beste Bildungssystem, Einfluss auf die Bildungspolitik zu nehmen; die rechtsgerichteten Unternehmer*innen, die Scholz & Friends bezahlen, fordern: a, b und c.

—Nicht der DLF

Full disclosure: Ich habe nicht versucht, die Studie zu lokalisieren oder gar rauszukriegen, was a, b und c in diesem speziellen Fall sein mögen, also auf welche Ideologeme hin die Metriken gestaltet wurden. Ich habe seit den 90er Jahren zu viele von Papieren dieses Genres gelesen, um noch im Geringsten auf dieses neugierig zu sein. Am Ende wird es halt wie üblich auf Privatisierung, mehr Industrieplunder in den Schulen, bevorzugt noch mit Staatsknete finanziert, und eine Brandmauer zwischen Schülis und fortschrittlichen Ideen rauslaufen.

Nur ein Datenpunkt zu „bestes“ und Sachsen: Die AfD hat bei der dortigen Landtagswahl 2019 28,4% der Stimmen bekommen, bei den gerade dem INSM-zertifiziert „besten“ Bildungssystem Deutschlands entwachsenen 18-24jährigen nach Aussage des MDR immer noch 19% (knapp hinter den Grünen mit 21%). Wenn das das Ergebnis des aus der Sicht reaktionärer UnternehmerInnen besten Bildungssystems ist, fällt es schwer, keine unangemessenen Parallelen zu ziehen.

Und wo ich schon von der INSM rede: Dass sich diese Leute nicht gelegentlich einen neuen Namen einfallen lassen, wundert mich sehr. Nachdem gerade die, die die INSM wohl am dringendsten beeinflussen möchte – junge Leute mit zumindest rudimentärem politischen Interesse – fast flächendeckend in Marc-Uwe Klings Känguru-Chroniken gelesen haben:

Initiative neue soziale Marktwirtschaft – Propagandanetzwerk des Schweinesystems. Vgl. dazu auch: Du bist Deutschland, Freundeskreis der Kernkraft, Anbeter des Arbeitsplatzes, Gläubige der Gleichschaltung,

würde ich an deren Stelle doch mal über eine, hust, Weiterentwicklung des, hust, Markenkerns nachdenken. Aber vielleicht verstehe ich auch nur nicht genug von Marketing.

⎆
Ach Bahn, Teil 9: Das Bahnhofs-WLAN

12022:238:1 ( 2022-08-26)
Hat jemand in den letzten drei Jahren vom Bahnhofs-Captive Portal mal irgendwas anderes gesehen als das hier?

Versteht wer das Bahnhofs-WLAN der Bahn? Ich habe das soeben aufgegeben, nachdem ich mir den „Verbindungsfehler“, den ich, glaube ich, seit vor Corona bei jedem Versuch der Verbindung mit Netzen mit der SSID WIFI@DB bekommen habe, genauer angesehen habe.

Natürlich sitzt auch auf diesen Netzen leider ein Captive Portal. Diese sind generell so gemacht, dass in dem Netz nach dem WLAN-Verbindungsaufbau erstmal alle HTTP-Requests auf (leider normalerweise horrös verjavascriptete – es gibt aber auch löbliche Ausnahmen) Provider-Seiten umgeleitet werden, auf denen mensch dann irgendeinen Quatsch abklicken soll. Ganz ehrlich: Ich habe diesen Quatsch noch nie gelesen, zumal ich glaube, dass er rechtlich nicht bindend ist und sowieso davon ausgehe, dass diese Netze mich aufs Kreuz legen wollen.

So weit, so ärgerlich. In WIFI@DB sieht es erstmal aus, als würde die Bahn das auch so machen:
```
$ curl -v http://blog.tfiu.de
[...]
< HTTP/1.1 302 Found
< Location: https://wifi.bahn.de/
```
Die Login-Seite wäre demnach wifi.bahn.de. Von dort sollte jetzt die Javascript-Grütze samt riesigen Bildern kommen, die mensch von grottigen Captive Portals gewöhnt ist. Aber nein:
```
$ curl -v https://wifi.bahn.de
[...]
< HTTP/1.0 302 Found
< Location: /sp/7cwojgdj/connectionError
```
Da wird mensch (bzw. computer) ganz platt gleich auf die Fehlerseite weitergeleitet – ok, da ist noch irgendeine Zeichenkette mit Trackinggeschmack dabei, die aber während meiner Experimente trotz variierender User Agents und MAC-Adressen konstant blieb. Um derwail mal was Nettes zu sagen: die Weiterleitung geht ganz ohne Javascript.

Die Fehlerseite selbst hat dann übrigens fast Captive Portal-Standard. Sie kommt mit minifiziertem jquery (zur Darstellung von „Verbindungsfehler“?!) und einem 2000 Pixel breiten JPEG (aber: nur 150k groß; normal ist alles unter 2 Megabyte sub-par für Captive Portals).

Wenn nun das mit der unmittelbaren Weiterleitung auf die Fehlerseite nur heute so wäre, würde ich sagen, gut, ist halt gerade kaputt. Aber wenn mich meine Erinnerung nicht sehr trügt, habe ich das schon lange nicht mehr anders gesehen.

Dass bei der Bahn das Außergewöhnliche normal ist, habe ich neulich schon festgestellt. Aber dass so Kram einfach immer kaputt ist, scheint mir doch etwas unplausibel. Hat wer eine Erklärung?
⎆
Schon die Werbung für Fahrradhelme schadet

12022:234:0 ( 2022-08-22)
Was RadlerInnen helfen soll: links Niederlande, rechts Australien. Ihr müsst wohl nicht lange nachdenken, wo mehr Leute radfahren – und wo AutofahrerInnen weniger von ihnen zermanschen.

Ich bin fest überzeugt, dass es Fahrradhelme ohne die Autolobby nicht gäbe; wichtigstes Indiz ist, dass der Anteil der HelmfahrerInnen stark korreliert ist mit der Rate zermanschter RadlerInnen pro geradeltem Kilometer. Das ist dann recht gut erklärbar, wenn Helmtragen und schlechte Bedingungen fürs Radfahren eine gemeinsame Ursache haben. Ein sehr naheliegender Kandidat für diese Ursache ist eine starke Autolobby (dort, wo es viele Helme gibt und also viel zermanscht wird).

Vielleicht kommt das etwas konspirologisch daher, aber es dreht den hervorragend recherchierten DLF-Hintergrund vom 10. August nur ein klein wenig weiter. Dessen Thema ist, wie Leute die Niederlande in das Fahrradparadies verwandelt haben, das sie (jedenfalls im Vergleich zu sonst fast allem) sind. So macht er beispielsweise den Punkt, dass Menschen in den 1970er und 1980er Jahren kräftig für die richtige Verkehrspolitik gerungen haben („es brauchte fast Straßenkämpfe in Amsterdam […], um das System zu ändern“), übrigens gegen erheblich stärkeren Widerstand als wir ihn heute haben. Die Nachricht, dass sich die Dinge nicht von selbst ändern, dass sie sich aber ändern lassen, finde ich höchst wichtig.

Im Hinblick auf die Helmfrage zitiert der Beitrag Meredith Glaser vom Urban Cycling Institute der Uni Amsterdam (Übersetzung DLF):

Die Forschung zeigt: Wenn es Gesetze gibt, die das Tragen von Helmen vorschreiben, dann geht die Fahrradnutzung zurück. Das hat sich auch in Kopenhagen gezeigt. Dort hat die Regierung eine gewisse Zeit lang für das Tragen von Helmen geworben. Und in diesem Zeitraum wurde weniger Fahrrad gefahren.

Vom Schaden der Helmpflicht wusste ich schon aus den Studien aus Australien (wo sie den Unfug, soweit ich weiß, immer noch nicht wieder aufgehoben haben); dass schon die Werbung schädlich ist, war mir neu. Um so naheliegender ist der Schluss der Sendung. Er kann aber nicht oft genug wiederholt werden, da ja nun die Autolobby ihre Sprüche auch unermüdlich daherbetet:

Eine Helmpflicht würde auch dazu führen, dass weniger Radfahrer auf den Straßen unterwegs wären. Und das wiederum habe dann tatsächlich Einfluss auf die Sicherheit der Radlerinnen und Radler.

Das ist der Grund für meine betretene Miene, wenn ich RadlerInnen mit Helmen sehe: Sie gefährden mein Leben.

Für den Fall, dass hier Helm-Fans vorbeikommen, will ich noch kurz auf ein paar irrige Argumente eingehen:
- „Na gut, dann hilft das Plastikding vielleicht nicht, wenn mensch vom Auto zermanscht wird, aber bei normalen Stürzen ist es doch super“ – nun, die Studienlage dazu ist, was Alltagsradeln angeht, allenfalls knapp über Globuli-Niveau. Das liegt daran, dass Alltagsradeln an sich eine recht sichere Angelegenheit ist. Wer nun in eine recht sichere Sache global eingreift, muss genau aufpassen, dass der Nutzen (d.h. leichtere Verletzungen bei der kleinen Klasse von Unfällen, bei denen der Helm wirkt) größer ist als die Summe der unerwünschten Nebenwirkungen (weniger vorsichtige Fahrweise, weniger Rücksicht durch Autofahrende, Fummeln am Helm zur falschen Zeit, erhöhte Umweltbelastung durch Produktion, Transport und Entsorgung der Helme, und natürlich: weniger Räder auf der Straße). Nur zur Sicherheit: Diese Abwägung mag bei tatsächlich gefährlichen Tätigkeiten („Sport“, hier: Rennradfahren; ggf. auch E-Bikes) anders ausgehen. Das normale Fahrrad aber zeichnet sich eben durch sein menschliches Maß aus.
- „Och, das sind dieselben Abwehrgefechte wie bei der Gurtpflicht oder der Helmpflicht für Motorradfahrer“ – Nein, sind sie nicht. Erstens, weil die Epidemiologie bei diesen beiden Maßnahmen ganz klar war: Es braucht keine großen Studien, um zu zeigen, dass bei den im motorisierten Individualverkehr (MIV) herrschenden Gewalten Menschen viel größere Überlebenschancen haben, wenn sie ordentlich Rüstung anlegen. Aber auch wenn Fahrradhelme erwiesenermaßen günstige Gesundheitseffekte hätten, wäre die Situation immer noch eine ganz andere, denn während es ein willkommener Effekt wäre, weniger Autos und Motorräder auf der Straße zu haben, hätte eine Verdrängung vom Fahrrad auf den MIV dramatisch negative Effekte auf die allgemeine Gesundheit (Lärm, Dreck, Bewegungsmangel, unzugänglicher öffentlicher Raum). Angesichts dessen müssten die Effekte bei Fahrradhelmen schon gigantisch sein, um ihre Einführung oder auch nur Bewerbung zu etwas anderem als einer menschenfeindlichen Operation zu machen.
- „Aber man kann doch Helm tragen und trotzdem was für besseren Fahrradverkehr tun.” – Klar. Wenn nicht Helme die Leute in die Autos treiben würden und die Leserbriefspalten bei jedem zermanschten Radler noch lauter „da, hätte er mal einen Helm getragen“ röhren würden, dann wäre es so oder so wurst. Aber so ist es nicht.
- Dein Argument hier – das Feedback-Formular wartet auf dich.
Bei der Gurtpflicht lohnt sich übrigens noch ein anderer Gedanke: Was wäre, wenn das autobedingte Blutvergießen damals nicht durch Aufrüstung (also Sicherung und stärkere Panzerung), sondern durch Abrüstung (also: global Tempo 30 für den MIV) angegangen worden wäre? Ich gehe hohe Wetten ein, dass das hunderttausende Leben gerettet hätte, ganz speziell welche ohne Lenkrad. Und wir hätten sehr wahrscheinlich viel weniger Autos auf den Straßen von heute. Wenn das international geklappt hätte, hätte es vielleicht sogar ein, zwei Zehntelgrad Klimaerwärmung ersparen können, zumal, wenn mensch einrechnet, dass es auf diese Weise wohl auch weniger Einfamilienhäuser gegeben hätte.

Das führt zwanglos auf die Schlüsse der Hintergrund-Sendung, die sich nämlich genau mit Visionen für den öffentlichen Raum beschäftigen. Es heißt dort, eine weniger durchgeknallte Verkehrspolitik würde bewirken, „dass Straßen dann wieder als öffentlicher Raum wahrgenommen würden und nicht nur als Verkehrssystem.“

Genau meine Rede.

Kommentar 1 am 2023-03-23

Selten so einen Quatsch gelesen.

Kommentar 2 am 2023-03-23 von Anselm

Hmja. Gegen so eine apodiktische Aussage ist schwer zu argumentieren. Was genau erscheint dir nicht begründet oder auch nur ernsthaft bestreitbar?
⎆
Adenauer vs. Ägypten: Frühe Einsichten zur Arbeit

12022:233:0 ( 2022-08-21)

Vielleicht passe ich gerade nur etwas besser auf, aber mir kommen derzeit besonders viele Fundstücke zum Thema Postwachstum und der Frage der Arbeit unter – die beiden sind ja, so behaupte ich, eng verbunden. Wenn wir nämlich wirklich in eine Gesellschaft übergehen, die den Menschen materielle Sicherheit bei einer minimalen Belastung von Natur und Mensch gewährleistet (und anders wird das wohl nichts mit der „Nachhaltigkeit“, vgl. Meadows ff von neulich), würden wir beim heutigen Stand der Produktivität locker mit zehn Stunden pro Woche Lohnarbeit auskommen – oder halt das, was in so einer Gesellschaft statt Lohnarbeit stattfinden würde.

Ein Beispiel für das genaue Gegenteil dieser aus meiner Sicht positiven Utopie war im DLF-Kalenderblatt vom 6.8. zu hören. Es erinnerte an die Eröffnung des ersten deutschen Autobahn-Teilstücks durch den Kölner Oberbürgermeister Konrad Adenauer. Fans von Volker Kutscher wissen das gleich zeitlich einzuordnen: Es war 1932. Die zentrale Nachricht des DLF-Beitrags sollte wohl sein, dass der postfaschistische Mythos von den Nazi-Autobahnen Quatsch ist. Für mich – da mir die Rubrizierung der Autobahnen als Nazimist eigentlich immer gut gepasst hat – viel eindrücklicher war aber die entspannte Selbstverständlichkeit, mit der der Potsdamer Historiker Ernst Piper in der Sendung die Aussage illustriert, der Autobahnbau sei eine „Maßnahme zur Bekämpfung der damaligen Massenarbeitslosigkeit“ gewesen.

Deswegen gab es zum Beispiel ja auch die Vorgabe – es galt auch für das kleine Stück, was Adenauer eingeweiht hat, das war dort genauso –, dass Maschinen nicht eingesetzt werden sollten. Es sollte alles, was irgend möglich war, mit Handarbeit erledigt werden, um möglichst viele Leute dort in Lohn und Brot zu bringen.

Ich finde es schlicht empörend, dass wir wegen der verrückten Religion von „wer nichts arbeitet, soll auch nichts essen“ Leute völlig sinnlos schinden. Mal abgesehen davon, dass netto die Menschheit wahrscheinlich besser dran wäre, wenn es keine Autobahnen gäbe und so die ganze Arbeit besser nicht gemacht worden wäre: Hätte, sagen wir, ein Zehntel der Leute mit ordentlichen Maschinen gearbeitet und die anderen, die da geschunden wurden, derweil vielleicht ein wenig gegärtelt und sich ansonsten ausgeruht, hätte es die Autobahn und wahrscheinlich sogar mehr Essen oder sonstwas Schönes oder Nützliches gegeben.

Die Schinderei hatte also auch dann überhaupt keinen Sinn, wenn die Autobahn als solche wertvoll gewesen wäre.

Dass dieser ziemlich ins Sadistische spielene Irrsinn noch nach 90 Jahren nicht zu einem Aufschrei der Empörung angesichts von solchen Mengen mutwilliger Zufügung von Leid führt, sagt, soweit es mich betrifft, viel darüber aus, wie viel Aufklärung noch zu besorgen ist gegen die Marktreligion und ihre Anhängsel.

Es mag etwas ironisch sein, dass ausgerechnet der Aberglaube im antiken Ägypten in diesem Punkt moderner, ehrlicher, aufgeklärter und nicht zuletzt pragmatischer wirkt. Gelernt habe ich das aber erst gestern, als ich im hessischen Landesmuseum in Darmstadt folgende Exponate sah:

Diese Tonfiguren sind Uschebtis. Zu deren Funktion erklärt die Wikipedia in Übereinstimmung mit den Angaben des Museums:

Wurde der Verstorbene nun im Jenseits zum Beispiel dazu aufgerufen, die Felder zu besäen oder die Kanäle mit Wasser zu füllen, so sollte der Uschebti antworten: „Hier bin ich.“ (6. Kapitel des Totenbuches). Damit der Uschebti die dem Toten aufgetragene Arbeit, insbesondere Feldarbeit, verrichten konnte, wurden ihm in älterer Zeit kleine Modelle der Geräte mitgegeben, die der Uschebti in den Händen hielt. In späterer Zeit wurden die Geräte auf die Figuren gemalt.

Ist das nicht großartig? Wie wenig ÄgypterInnen mit der modernen (und nein, Herr Weber, nicht nur protestantischen) Arbeitsmoral anfangen konnten, lässt sich an der Unmenge von Uschebtis ablesen, die wir noch nach 3000 Jahren finden. Die Museums-Leute haben erzählt, die Dinger seien im 19. Jahrhundert sehr populäre Mitbringsel von Ägypten-Urlauben gewesen, denn sie seien eigentlich überall zu finden gewesen.

Klar, außerhalb ökonomischer Diskussionen sind sich auch heute alle einig, dass Lohnarbeit stinkt – vgl. die „Endlich Freitag“-Spots der ARD –, aber kaum zwei Ecken weiter kommt doch wieder die fast nie öffentlich in Frage gestellte Gegenunterstellung, ein Leben ohne Lohnarbeit müsse traurig und sinnlos sein (wäre das so, würde das, wie schon Bertrand Russell bemerkt hat, ein sehr schlechtes Licht auf unser Bildungssystem werfen). Zumindest diesen Unfug hat es schon im ägyptischen Totenbuch nicht mehr gegeben.

Dass wir 4500 Jahre nach dessen ersten Anfängen wieder Mühe haben, diese Dinge klar zu kriegen, zeigt erneut, dass der Prozess der Zivilisation schwierig ist und es immer wieder Rückschläge gibt.

Übrigens will ich natürlich mitnichten zurück zu ägyptischen Praktiken. Abgesehen davon, dass die Herstellung der Uschebtis zweifellos in die Klasse der wirtschaftlichen Aktivitäten fällt, deren Einstellung die Welt besser gemacht hätte: Die Sitte, die zunächst so sympathisch wirkt (solange mensch nicht ans Totenreich oder jedenfalls die Leidensfähigkeit von Tonfiguren glaubt), hat sich im Laufe der Jahrhunderte in Weisen entwickelt, die an moderne Freihandelszeiten erinnert. Nochmal die Wikipedia:

Während es in der 18. Dynastie meist nur einzelne Exemplare waren, konnte die Anzahl in der Spätzeit weitaus höher sein. [...] Ab dem Ende der 18. Dynastie, vom Höhepunkt des Neuen Reiches bis zu den Ptolemäern, wurden sie durch Aufseherfiguren ergänzt [...] Der Aufseher hatte zu überwachen, dass der Uschebti die Arbeiten ordnungsgemäß durchführte. Er wurde dafür mit Stock und Peitsche ausgeführt.

⎆
How to Block a USB Port on Smart Hubs in Linux

12022:232:1 ( 2022-08-20)
Somewhere beneath the fan on the right edge of this image there is breakage. This post is about how to limit the damage in software until I find the leisure to dig deeper into this pile of hitech.

My machine (a Lenovo X240) has a smart card reader built in, attached to its internal USB. I don't need that device, but until a while ago it did not really hurt either. Yes, it may draw a bit of power, but I'd be surprised if that were more than a few milliwatts or, equivalently, one level of screen backlight brightness; at that level, not even I will bother.

However, two weeks ago the thing started to become flaky, presumably because the connecting cable is starting to rot. The symptom is that the USB stack regularly re-registers the device, spewing a lot of characters into the syslog, like this:
```
Aug 20 20:31:51 kernel: usb 1-1.5: USB disconnect, device number 72
Aug 20 20:31:51 kernel: usb 1-1.5: new full-speed USB device number 73 using ehci-pci
Aug 20 20:31:52 kernel: usb 1-1.5: device not accepting address 73, error -32
Aug 20 20:31:52 kernel: usb 1-1.5: new full-speed USB device number 74 using ehci-pci
Aug 20 20:31:52 kernel: usb 1-1.5: New USB device found, idVendor=058f, idProduct=9540, bcdDevice= 1.20
Aug 20 20:31:52 kernel: usb 1-1.5: New USB device strings: Mfr=1, Product=2, SerialNumber=0
Aug 20 20:31:52 kernel: usb 1-1.5: Product: EMV Smartcard Reader
Aug 20 20:31:52 kernel: usb 1-1.5: Manufacturer: Generic
Aug 20 20:31:53 kernel: usb 1-1.5: USB disconnect, device number 74
Aug 20 20:31:53 kernel: usb 1-1.5: new full-speed USB device number 75 using ehci-pci
[as before]
Aug 20 20:32:01 kernel: usb 1-1.5: new full-speed USB device number 76 using ehci-pci
Aug 20 20:32:01 kernel: usb 1-1.5: New USB device found, idVendor=058f, idProduct=9540, bcdDevice= 1.20
Aug 20 20:32:01 kernel: usb 1-1.5: New USB device strings: Mfr=1, Product=2, SerialNumber=0
[as before]
Aug 20 20:32:02 kernel: usb 1-1.5: USB disconnect, device number 76
```
And that's coming back sometimes after a few seconds, sometimes after a few 10s of minutes. Noise in the syslog is never a good thing (even when you don't scroll syslog on the desktop), as it will one day obscure something one really needs to see, and given that device registrations involve quite a bit of computation, this also is likely to become relevant power-wise. In short: this has to stop.

One could just remove the device physically or at least unplug it. Unfortunately, in this case that is major surgery, which in particular would involve the removal of the CPU heat sink. For that I really want to replace the thermal grease, and I have not been to a shop that sells that kind of thing for a while. So: software to the rescue.

With suitable hubs – the X240's internal hub with the smart card reader is one of them – the tiny utility uhubctl lets one cut power to individual ports. Uhubctl regrettably is not packaged yet; you hence have to build it yourself. I'd do it like this:
```
sudo apt install git build-essential libusb-dev
git clone https://github.com/mvp/uhubctl
cd uhubctl
prefix=/usr/local/ make
sudo env prefix=/usr/local make install
```
After that, you have a program /usr/local/sbin/uhubctl that you can run (as root or through sudo, as it needs elevated permissions) and that then tells you which of the USB hubs on your system support power switching, and it will also tell you about devices connected. In my case, that looks like this:
```
$ sudo /usr/local/sbin/uhubctl
Current status for hub 1-1 [8087:8000, USB 2.00, 8 ports, ppps]
  Port 1: 0100 power
  [...]
  Port 5: 0107 power suspend enable connect [058f:9540 Generic EMV Smartcard Reader]
  [...]
```
This not only tells me the thing can switch off power, it also tells me the flaky device sits on port 5 on the hub 1-1 (careful inspection of the log lines above will reconfirm this finding). To disable it (that is, power it down), I can run:
```
$ sudo /usr/local/sbin/uhubctl -a 0 -l 1-1 -p 5
```
(read uhubctl --help if you don't take my word for it).

Unfortunately, we are not done yet. The trouble is that the device will wake up the next time anyone touches anything in the wider vicinity of that port, as for instance run uhubctl itself. To keep the system from trying to wake the device up, you also need to instruct the kernel to keep its hands off. For our port 5 on the hub 1-1, that's:
```
$ echo disabled > /sys/bus/usb/devices/1-1.5/power/wakeup
```
or rather, because you cannot write to that file as a normal user and I/O redirection is done by your shell and hence wouldn't be influenced by sudo:
```
$ echo disabled | sudo tee /sys/bus/usb/devices/1-1.5/power/wakeup
```
That, indeed, shuts the device up.

Until the next suspend/resume cycle that is, because these settings do not survive across one. To solve that, arrange for a script to be called after resume. That's simple if you use the excellent pm-utils. In that case, simply drop the following script into /etc/pm/sleep.d/30killreader (or so) and chmod +x the file:
```
#!/bin/sh
case "$1" in
  resume|thaw)
    echo disabled > /sys/bus/usb/devices/1-1.5/power/wakeup
    /usr/local/sbin/uhubctl -a 0 -l 1-1 -p 5
    ;;
esac
exit 0
```
If you are curious what is going on here, see /usr/share/doc/pm-utils/HOWTO.hooks.gz.

However, these days it is rather unlikely that you are still leaving suspend and hibernate to pm-utils; instead, on your box this will probably be handled by systemd-logind. You could run pm-utils next to that, I suppose, if you tactfully configured the host of items with baroque names like HandleLidSwitchExternalPower in logind.conf, but, frankly, I wouldn't try that. Systemd's reputation for wanting to manage it all is not altogether undeserved.

I have tried to smuggle in my own code into logind's wakeup procedures years ago in systemd's infancy and found it hard if not impossible. I'm sure it is simpler now. If you know a good way to make logind run a script when resuming: Please let me know. I promise to amend this post for the benefit of people running systemd (which, on some suitable boxes, does include me).
⎆
Und nochmal Postwachstum: Von Friedrichstadt zu Isnogud

12022:227:9 ( 2022-08-16)

Als ich vor gut einem Monat Friedrichstadt als Modell für eine gemütliche und hübsche Postwachstumsgesellschaft gelobt habe, habe ich auf eine wirklich augenfällige Besonderheit des Ortes nicht hingewiesen: Vor fast allen Häusern wachsen auf kleinstem Raum sorgfältig gepflegte Blumen, zumeist Rosen. Hier drei keineswegs untypische Beispiele:

Nun glaube ich nicht, dass der Mensch zum Wettbewerb geboren ist – dass es spätestens auf Schulhöfen so aussehen mag, lässt sich zwanglos als Herausforderung im Prozess der Zivilisation auffassen. Solange aber die soziale Praxis ist, wie sie ist, finde ich die Friedrichstädter Ableitung von Wettbewerbstrieb in eine dekorative und weitgehend unschädliche Richtung eine großartige Strategie zur, hust, Nachhaltigkeit (Übersetzung aus dem Blablaesischen: Das können sie auch noch 1000 Jahre so treiben, ohne dass es ihnen um die Ohren fliegt).

Wenn die Menschen hingegen darum wettbewerben, wer das größere Auto hat oder, noch viel schlimmer, wessen Unternehmen mehr produziert, hat das ganz offensichtlich dramatische Konsequenzen; in einer Art individualpsychologischer Kapitalismusanalyse würde es sogar taugen, die ganze Wachstumskatastrophe zu erklären.

Allerdings machen manche der Friedrichstädter Blumen durchaus den Eindruck, als hätten sie Dünger auf Mineralölbasis bekommen oder auch fiese Pestizide, so dass bei so einem Herumdoktorn an Symptomen des Wettbewerbswahnsinns jedenfalls Vorsicht nötig ist. Sobald die Leute nämlich in ihrer Wettbewerberei immer größere Flächen düngen oder begiften können, ist es schon wieder vorbei mit der, hust, Nachhaltigkeit. Ich denke, das ist meine Chance, das neueste der wunderbaren Worte, die wir der Nuklearlobby zu verdanken haben, in meinen aktiven Wortschatz aufzunehmen:

Wir sollten Rosenzucht wie in Friedrichstadt als Streckbetrieb der Wettbewerbsgesellschaft denken.

—Anselm Flügel (2022)

Die Friedrichstadt-Thematik ist aber eigentlich nur Vorgeplänkel, denn wirklich verweisen wollte ich auf den Artikel „Bevölkerungswachstum – Wie viele werden wir noch?“ von David Adam im Spektrum der Wissenschaft 2/2022 (S. 26; Original in Nature 597 (2021), S. 462), der mir vorhin in die Hände gefallen ist.

Diesen Artikel fand ich schon deshalb bemerkenswert, weil er recht klar benennt, dass ein Ende des Wachstums (in diesem Fall der Bevölkerung) wünschenswert und zudem auch fast unvemeidlich ist, sobald Frauen über ihre Fortpflanzung hinreichend frei entscheiden können und sich Religion oder Patriotismus oder Rassismus nicht zu stark verdichten. Vor allem aber wird dort eine große Herausforderung für fortschrittliche Menschen angekündigt:

In 23 Ländern könnte sich die Bevölkerung laut dieser Vorhersage bis Ende des Jahrhunderts sogar halbiert haben, unter anderem in Japan, Thailand, Italien und Spanien.

Ich bin überzeugt, dass sich die wenigsten MachthaberInnen mit so einer Entwicklung abfinden werden, so willkommen sie gerade in diesen dicht besiedelten Staaten (gut: Spanien und Thailand spielen mit um die 100 Ew/km² schon in einer harmloseren Liga als Japan oder Baden-Württemberg mit um die 300) auch sind. Menschen mit Vernunft und ohne Patriotismus werden dann sehr aufdringlich argumentieren müssen, dass Bevölkerungsdichten von 50 oder auch nur 10 Menschen auf dem Quadratkilometer das genaue Gegenteil vom Ende der Welt sind und jedenfalls für ein paar Halbierungszeiten überhaupt kein Anlass besteht, darüber nachzudenken, wie Frauen, die keine Lust haben auf Schwangerschaft und Kinderbetreuung, umgestimmt werden könnten.

Wie würde ich argumentieren? Nun, zunächst mal in etwa so:

Die kulturelle Blüte unter Hārūn ar-Raschīd (um mal eine recht beeindruckende Hochkultur zu nennen; siehe auch: Isnogud) fand in einer Welt mit höchstens 300 Millionen Menschen statt, also rund einem sechzehntel oder 2^− 4 der aktuellen Bevölkerung. Angesichts der damaligen Gelehrsamkeit dürfte als sicher gelten, dass mit so relativ wenigen Menschen immer noch eine interessante (technische) Ziviliation zu betreiben ist. Demnach haben wir mindestens vier Halbierungszeiten Zeit, ohne dass unsere Fähigkeit, in der Breite angenehm zu leben, aus demographischen Gründen in Frage steht.

Wenn unsere modernen Gesellschaften von Natur aus um 1% im Jahr schrumpfen würden, wäre eine Halbierungszeit etwa 75 Jahre, und die vier Halbierungszeiten würden zu 300 Jahren, in denen wir uns wirklich in aller Ruhe überlegen könnten, wie wir unsere Reproduktion so organisieren, dass Frauen im Schnitt auch wirklich die 2.1 Kinder bekommen wollen, die es für eine stabile Bevölkerungszahl bräuchte (oder wie wir die Bevölkerungszahl anders stabilisiert kriegen; soweit es mich betrifft, ist ja auch die ganze Sterberei deutlich überbewertet).

Allerdings ist das wahrscheinlich ohnehin alles müßig. Zu den bedrückendsten Papern der letzten 20 Jahre gehört für mich A comparison of The Limits to Growth with 30 years of reality von Graham Turner, erschienen in (leider Elsevier) Global Environmental Change 18 (2008), 397 (doi:10.1016/j.gloenvcha.2008.05.001; bei libgen). Darin findet sich folgende Abbildung:

Copyright 2008 Elsevier (Seufz! Das Mindeste wäre ja, dass die Rechte bei denen liegen, die die Forschung bezahlt haben, in diesem Fall also der CSIRO)

Was ist da zu sehen? Die Kuven in grün und rot geben jeweils die Umweltverschmutzungs-Metrik der Modelle, die Dennis Meadows et al um die 1970 herum gerechnet haben und die zur Publikation der Grenzen des Wachstums geführt haben. Rot ist dabei das Modell, in dem es glaubhafte technische Bemühungen um Umweltschutz gibt, ansonsten aber weiter Wachstumskurs herrscht. Die grüne Kurve zeigt das Modell, in dem Leute allenfalls so tun als ob.

Dass mit „Grünem Wachtum“ (in einem Wort: Elektroautos) die totale Umweltverschmutzung einen viel höheren Peak nimmt (wenn auch später), ist schon mal eine Einsicht, an die sich nicht mehr viele erinnern wollen; Meadows et al teilen jedenfalls meine Einschätzung, dass es keine technische Lösung für das Problem der Endlichkeit des Planeten gibt. Wer sowas dennoch versucht, sollte wissen, worum es geht: Die Umweltverschmutzung geht in den Modellen nach den Gipfeln zurück, weil die Umweltverschmutzenden (a.k.a. die Menschen) in großer Zahl (zu mehr als 2/3) verhungert, an Seuchen oder sonst irgendwie vor ihrer Zeit gestorben sind.

So viel war schon vor Turners schlimmem Paper klar. Turners Beitrag war nun, reale Messgrößen auf Meadows' Metriken abzubilden – darüber ließe sich, wie immer bei Metriken, sehr trefflich streiten. Akzeptiert mensch diese Abbildung jedoch, ist die reale Entwicklung durch die schwarzen Punkte knapp unter der grünen Kurve repräsentiert. Das würde heißen: für die 30 Jahre zwischen 1970 und 2000 kommt eines von Meadows Modellen ziemlich genau hin: Das Modell, das in den 2030er Jahren kippt.

Und nochmal: „Kippen“ ist hier ein terminus technicus dafür, dass etwas wie zwei von drei Menschen innerhalb von grob einem Jahrzehnt sterben.

Wenn sich Meadows und Turner nicht ordentlich verrechnet haben – und ja, ich hätte an beiden Arbeiten reichlich zu meckern, nur wohl leider nicht genug, um die grundsätzlichen Ergebnisse ernsthaft zu bestreiten –, wird in gut zehn Jahren die Frage eines düsteren 80er Jahre-Graffitos in einer Erlanger Unterführung brandaktuell:

Who will survive? And what will be left of them?

—Ungefähr hier

⎆
Ach Bahn, Teil 8: Das Außergewöhnliche als Normalzustand

12022:218:0 ( 2022-08-06)

Ich wollte heute eine Bahnfahrkarte nach Hamburg kaufen. Die Verbindungssuche sah aus wie im Bild nebenan (bzw. obendrüber): Für praktisch alle Züge erwartet die Bahn eine „Außergewöhnlich hohe Auslastung“. Das hat mich zum Nachdenken über den Begriff „außergewöhnlich“ gebracht. Wenn etwas praktisch immer gilt, wäre es dann nicht ehrlicher, „wie üblich knallvoll (und das, obwohl wir den Nahverkehr im Augenblick praktisch verschenken)“ zu sagen?

Und ja, ich habe dabei vorläufig die Fantasie aufgegeben, dass die Bahn einfach ein paar neue Wagen kauft und an die Züge dranhängt oder gar engeren Takt fährt – beides wäre ja, Willen, etwas technische Flexibilität und evtl. die Bereitschaft, nicht unbedingt so zu rasen vorausgesetzt, möglich und darüber hinaus für einen „Mobilitätsdienstleister“ (gewiss nicht mein Wort) auch recht naheliegend, wenn eine Strecke dauerhaft oder auch nur regelmäßig so „außergewöhntlich“ überlastet ist. Aber das wird wohl warten müssen, bis wir eines Tages die gute alte BeamtInnenbahn wiederbekommen. Oder, gasp, noch was Besseres.

Ich habe übrigens am Schluss gar keine Fahrkarte bekommen. Zunächst hat mich die Bahn schon wieder mit Captchas belästigt, wobei die Schurken des Bahn-Auftragsdatenverarbeiters hcaptcha fast selbstironisch zunächst verlangten: „Klicken Sie Bilder mit lachenden Hunden an“. Echt. Ich bereue immer noch, nicht an einen Screenshot gedacht zu haben. Kleiner Tipp an hcaptcha: Hunde haben überhaupt keine Muskulatur, die ihnen Lachen erlauben würde. PSA: Bären auch nicht.

Na ja, und nachdem ich mich zu Giraffen durch- und ungefähr 12 von denen angeklickt hatte, hat mir der Bahnserver eine nginx-Fehlermeldung „too many connections“ geliefert (aber ich will nicht undankbar sein: es war aufregenderweise vernünftiges HTML von einer Bahn-Seite).

Geheimtipp: Wer bei der Verbindungssuche „schnellste Verbindung“ abklickt, bekommt auch einen IC angeboten. Der fährt zwar noch wahrscheinlicher nicht als der ICE, und wenn er fährt, wird er knapp zwei Stunden länger brauchen. Aber er wird wahrscheinlich über weite Strecken erheblich leerer sein, vermutlich trotzdem weniger Strom verbrauchen, und mehr zu sehen gibts auch.

⎆
SPARQL 4: Be Extra Careful on your Birthday

12022:217:0 ( 2022-08-05)
Enough Yak Shaving already.
I am now three parts into my yak-shaving investigation of Wikidata and SPARQL (one, two, three) with the goal of figuring out whether birthdays are more or less dangerous – measured by whether or not people survive them – than ordinary days.

At the end of the last instalment I was stumped by timeouts on Wikidata, and so much of this post is about massaging my query so that I get some answers in the CPU minute that one gets on Wikidata's triplestore. While plain optimisation certainly is necessary, working on six million people within a minute is probably highly ambitious whatever I do[1]. I will hence have to work on a subset. Given what I have worked out in part 3,
```
# This will time out and just waste CPU.
SELECT (count(?person) AS ?n)
WHERE {
  ?person rdfs:label ?personName.
  ?person wdt:P569 ?bdate.
  hint:Prior hint:rangeSafe true.
  ?person wdt:P570 ?ddate.
  hint:Prior hint:rangeSafe true.

  FILTER (MONTH(?bdate)>1 || DAY(?bdate)>1)
  FILTER (MONTH(?bdate) = MONTH(?ddate)
    && DAY(?bdate) = DAY(?ddate)
    && YEAR(?bdate) != YEAR(?ddate))
  FILTER (YEAR(?bdate)>1850)

  FILTER (lang(?personName)="en")
}
```
– how do I do a subset? Proper sampling takes almost as much time as working with the whole thing. But for now, I'd be content with just evaluating my query on whatever subset Wikidata likes to work on. Drawing such a (statiscally badly sampled) subset is what the LIMIT clause you have already seen in part one does. But where do I put it, since, if things work out, my query would only return a single row anyway?
Subqueries in SPARQL, and 50 Labels per Entity

The answer, as in SQL, is: A subquery. In SPARQL, you can have subqueries like this:
```
SELECT (count(?person) as ?n)
WHERE {
  { SELECT ?person ?personName ?bdate ?ddate
    WHERE {
      ?person rdfs:label ?personName;
        wdt:P569 ?bdate;
        wdt:P570 ?ddate.
    }
    LIMIT 50
  }
  FILTER (lang(?personName)="en")
}
```
– so, within a pair of curly braces, you write another SELECT clause, and its is then the input for another WHERE, FILTER, or other SPARQL construct. In this case, by the way, I'm getting 50 records with all kinds of labels in the subquery and then filter out everything that's not English. Amazingly, only one record out of these 50 remains: there are clearly at least 50 statements on labels for the first entity Wikidata has picked here.

Raising the innner limit to 500, I get 10 records. For the particular sample that Wikidata chose for me, a person indeed has 50 labels on average. Wow. Raising the limit to 5000, which probably lowers the the pharaohs to non-pharaohs in the sample, gives 130 records, which translates into 38 labels per person.

Clearly, adding the labels is an expensive operation, and since I do not need them for counting, I will drop them henceforth. Also, I am doing my filtering for off-January 1st birthdays in the subquery. In this way, I probably have a good chance that everything coming out of the subquery actually counts in the outer filter, which means I can compute the rate of people dying on their birthday by dividing my count by the limit.

Let's see where this gets us:
```
SELECT (count(?person) AS ?n)
WHERE {
  { SELECT ?person ?bdate ?ddate
    WHERE {
      ?person wdt:P569 ?bdate.
      hint:Prior hint:rangeSafe true.
      ?person wdt:P570 ?ddate.
       FILTER (MONTH(?bdate)>1 || DAY(?bdate)>1)
      FILTER (YEAR(?bdate)>1850)
      hint:Prior hint:rangeSafe true.
    }
    LIMIT 500
  }

  FILTER (MONTH(?bdate) = MONTH(?ddate)
    && DAY(?bdate) = DAY(?ddate)
    && YEAR(?bdate) != YEAR(?ddate))
  hint:Prior hint:rangeSafe true.
}
```
Named Subqueries and Planner Barriers

That's returning a two for me, which is not implausible, but for just 500 records it ran for about 20 seconds, which does not feel right. Neither pulling the 500 records nor filtering them should take that long.

When a database engine takes a lot longer than one thinks it should, what one should do is take look at the query plan, in which the database engine states in which sequence it will compute the result, which indexes it intends to use, etc.

Working out a good query plan is hard, because in general you need to know the various partial results to find one; in my example, for instance, the system could first filter out everyone born after 1850 and then find the death dates for them, or it could first match the death dates to the birthdays (discarding everything that does not have a death day in the process) and then filter for 1850. Ff there were may people with birthdays but no death days (for instance, because your database talks mostly about living people), the second approach might be a lot faster. But you, that is, the database engine, have to have good statistics to figure that out.

Since that is such a hard problem, it is not uncommon that the query planner gets confused and re-orders operations such that things are a lot slower than they would be if it hadn't done the ordering, and that's when one should use some sort of explain feature (cf. Wikidata's optimisation hints). On Wikidata, you can add an explain=detail parameter to the query and then somehow display the bunch of HTML you get back.

I did that and, as I usually do when I try this kind of thing, found that query plans are notoriously hard to understand, in particular when one is unfamiliar with the database engine. But in the process of figuring out the explain thing, I had discovered that SPARQL has the equivalent of SQL's common table expressions (CTEs), which gave me an excuse to tinker rather than think about plans. Who could resist that?

In SPARQL, CTEs are called named subqueries and used like this:
```
SELECT (count(?person) AS ?n)
WITH { SELECT ?person ?bdate ?ddate
    WHERE {
      ?person wdt:P569 ?bdate;
      hint:Prior hint:rangeSafe true.
      ?person wdt:P570 ?ddate.
      hint:Prior hint:rangeSafe true.
       FILTER (MONTH(?bdate)>1 || DAY(?bdate)>1)
      FILTER (YEAR(?bdate)>1850)
    }
    LIMIT 30000
  } AS %selection
WHERE {
  INCLUDE %selection

  FILTER (MONTH(?bdate) = MONTH(?ddate)
    && DAY(?bdate) = DAY(?ddate)
    && YEAR(?bdate) != YEAR(?ddate))
  hint:Prior hint:rangeSafe true.
```
– you write your subquery in a WITH-block and give it a name that you then INCLUDE in your WHERE clause. In several SQL database systems, such a construct provides a planner barrier, that is, the planner will not rearrange expressions across a WITH.

So does, according to the optimisation hints, Wikidata's current SPARQL engine. But disappointingly, things don't speed up. Hmpf. Even so, I consider named subexpresisons more readable than nested ones[2], so for this post, I will stay with them. In case you come up with a brilliant all-Wikidata query, you probably want to go back to inline subqueries, though, because then you probably do not want to constrain the planner too much.
Finally: Numbers. But what do they Mean?

With my barrier-protected subqueries, I have definitely given up on working with all 6 million persons with birthdays within Wikidata. Interestingly, I could go from a limit of 500 to one of 30'000 and stay within the time limit. I never went back to try and figure out what causes this odd scaling law, though I'd probably learn a lot if I did. I'd almost certainly learn even more if I tried to understand why with a limit of 50'000, the queries tended to time out. But then 30'000 persons are plenty for my purpose provided they are drawn reasonably randomly, and hence I skipped all the tempting opportunities to learn.

And, ta-da: With the above query, I get 139 matches (i.e., people who died on their birthdays).

What does that say on the danger of birthdays? Well, let's see: If birthdays were just like other days, one would expect 30'000/365 deaths on birthdays in this sample, which works out to a bit more than 80. Is the 140 I am finding different from that 80 taking into account statistical noise? A good rule of thumb (that in the end is related to the grand central limit theorem) is that when you count n samples, your random error is something like √(n) if everything is benevolent. For 140, that square root is about 12, which we physicist-hackers like to write as σ = 12, and then we quickly divide the offset (i.e., 140 − 80 = 60) by that σ and triumphantly proclaim that “we've got a 5-σ effect”, at which point everyone is convinced that birthdays are life-threatening.

This is related to the normal distribution (“Gauss curve”) that has about 2/3s of its area within “one σ” (which is its width as half maximum and would be the standard deviation of something you draw from such a distribution), 95% of …
⎆
SPAQRL 3: Who Died on their Birthdays?

12022:216:0 ( 2022-08-04)
A lot of Yak Shaving left to do here.
Now that I have learned how to figure out dates of birth and death in Wikidata and have made myself sensible tools to submit queries, I can finally start to figure out how I can let Wikidata pick out people dying on the same day of the year they were born on, just like Mary Lea Heger.

I first fetched people with their birthdays and dates of death:
```
SELECT ?person ?bday ?dday
WHERE {
  ?person wdt:P569 ?bday.
  ?person wdt:P570 ?dday.
}
LIMIT 2
```
Consider that query for a while and appreciate that by giving two triple patterns using the same variable, ?person, I am performing what in SQL databases would be a join. That that's such a natural thing in SPARQL is, I'd say, a clear strong point for the language.

Here is what I got back when I ran this this through my wpd shell function from part two:
```
person=http://www.wikidata.org/entity/Q18722
dday=-1871-06-29T00:00:00Z
bday=-2000-01-01T00:00:00Z

person=http://www.wikidata.org/entity/Q18734
dday=-1884-01-01T00:00:00Z
bday=-2000-01-01T00:00:00Z
```
This seems to work, except the dates look a bit odd. Did these people really die more than a hundred years before they were born? Ah, wait: these are negative dates. Opening the person URIs as per part one in a browser, I one learns that Q18722 is pharaoh Senusret II, and at least his birthday clearly is… not very certain. If these kinds of estimates are common, I probably should exclude January 1st from my considerations.
Getting Labels

But the first thing I wanted at that point was to not have to click on the URIs to see names. I knew enough about RDF to simply try and get labels according to RDF schema:
```
SELECT ?personName ?bday ?dday
WHERE {
  ?person rdfs:label ?personName.
  ?person wdt:P569 ?bday.
  ?person wdt:P570 ?dday.
}
LIMIT 10
```
That's another SQL join, by the way. Nice. Except what comes back is this:
```
dday=-2596-01-01T00:00:00Z
bday=-2710-01-01T00:00:00Z
personName=Хуан-ди

dday=-2596-01-01T00:00:00Z
bday=-2710-01-01T00:00:00Z
personName=Huang Di

dday=-2596-01-01T00:00:00Z
bday=-2710-01-01T00:00:00Z
personName=ኋንግ ዲ

dday=-2596-01-01T00:00:00Z
bday=-2710-01-01T00:00:00Z
personName=هوان جي دي

dday=-2596-01-01T00:00:00Z
bday=-2710-01-01T00:00:00Z
personName=Emperador mariellu
```
If you select the URI in ?person in addition to just the name, you'll see that we now got many records per person. Actually, one per label, as is to be expected in a proper join, and since there are so many languages and scripts out there, many persons in Wikidata have many labels.

At this point I consulted Bob DuCharme's Learning SPARQL and figured a filter on the language of the label is what I wanted. This does not call for a further join (i.e., triple pattern), as the language is something like a property of the object literal (i.e., the string) itself. To retrieve it, there is a function determining the language, used with a FILTER clause like this:
```
SELECT ?personName ?bday ?dday
WHERE {
  ?person rdfs:label ?personName.
  ?person wdt:P569 ?bday.
  ?person wdt:P570 ?dday.

  FILTER (lang(?personName)="en")
}
LIMIT 10
```
FILTER is a generic SPARQL thing that is more like a SQL WHERE clause than SPARQL's WHERE clause itself. We will be using it a lot more below.

There is a nice alternative to this kind of joining and filtering I would have found in the wikidata user manual had I read it in time. You see, SPARQL also defines a service interface, and that then allows queriers to mix and match SPARQL-speaking services within a query. Wikidata has many uses for that, and one is a service that can automatically add labels with minimal effort. You just declare that you want that service to filter your query, and then you write ?varLabel to get labels instead of URIs for ?var, as in:
```
# don't run this.  It'll put load on Wikidata and then time out
SELECT ?personLabel ?bday ?dday
WHERE {
  ?person wdt:P569 ?bday.
  ?person wdt:P570 ?dday.

  SERVICE wikibase:label {
    bd:serviceParam wikibase:language "en" .
  }
}
LIMIT 10
```
The trouble with that: This would first pull out all result triples (a couple of million) out of wikidata and then hand over these triples to the wikibase:label service, which would then add the labels and hand back all the labelled records. Only then will the engine discard the all result rows but the first 10. That obviously is terribly inefficient, and Wikidata will kill this query after a minute.

So: Be careful with SERVICE when intermediate result sets could be large. I later had to use subqueries anyway; I could have used them here, too, to work around the millions-of-triples problem, but at that point I hadn't progressed to these subqueries, let alone means to defeat the planner (that's part four material).
Determining Day and Month

Turtle (about my preference for which you could already read in part two) has a nifty abbreviation where you can put a semicolon after a triple and then leave out the subject in the next triple. SPARQL will put the previous subject into this next triple. That works in SPARQL, too, so I can write my query above with fewer keystrokes:
```
SELECT ?personName ?bday ?dday
WHERE {
  ?person rdfs:label ?personName;
    wdt:P569 ?bday;
    wdt:P570 ?dday.

  FILTER (lang(?personName)="en")
}
LIMIT 10
```
Now I need to figure out the birthday, as in: date within a year. In Bob DuCharme's book I found a SUBSTR function, and BIND clauses that let you compute values and bind them to variables. Treating the dates as ISO strings (“YYYY-MM-DD“) should let me pull out month and date starting at index 6 (gna: SPARQL starts with index 1 rather than with 0 as all deities in known history wanted), and then five characters, no? Let's see:
```
SELECT ?personName ?bdate ?ddate
 WHERE {
   ?person rdfs:label ?personName;
     wdt:P569 ?bday;
     wdt:P570 ?dday.

   BIND (SUBSTR(?bday, 6, 5) as ?bdate)
   BIND (SUBSTR(?dday, 6, 5) as ?ddate)

   FILTER (lang(?personName)="en")
 }
 LIMIT 3
```
This gives:
```
personName=Sobekhotep I
bdate=-01-0
ddate=-01-0

personName=Amenemhat I
ddate=-02-1

personName=Senusret II
bdate=-01-0
ddate=-06-2
```
Well, that is a failure. And that's because my assumptions on string indices are wrong in general, that is: for people born before the Christian era, and then again for people born after 9999-12-31. Which makes we wonder: Does Wikidata have people born in the future? Well, see below.

I'll cheat a bit and spare you a few of the dead alleys I actually followed trying to fix this, because they are not very educational. Also, when I strugged with the timeouts I will discuss in a moment I learned about the right way to do this on Wikidata's optimisation page: When something is a date, you can apply the functions DAY, MONTH, and YEAR on it, and that will plausibly even use indexes and thus be a lot faster.

Thinking about YEAR and having seen the fantasy dates for the ancient Egyptian pharaohs, I also decided to exclude everyone before 1850; that ought to suffice for letting me forget about Gregorian vs. Julian dates, and the likelihood that the dates are more or less right ought to be a lot higher in those days than in the 14th century, say.

With that, I can write the “birth day equals death day“ in a filter without further qualms. The resulting query is starting to look imposing:
```
SELECT ?person ?personName ?bdate ?ddate
WHERE {
  ?person rdfs:label ?personName.
  ?person rdfs:label  wdt:P569 ?bdate.
  hint:Prior hint:rangeSafe true.
  ?person rdfs:label wdt:P570 ?ddate.
  hint:Prior hint:rangeSafe true.

  FILTER (MONTH(?bdate) = MONTH(?ddate)
    && DAY(?bdate) = DAY(?ddate))
  FILTER (YEAR(?bdate)>1850)

  FILTER (lang(?personName)="en")
}
LIMIT 10
```
The odd triples with hint:Prior are hints for Wikidata's triple store that, or so I understand Wikidata's documentation, encourages it to use indexes on the properties mentioned in the previous lines; the query certainly works without those, and I frankly have not bothered to see if they actually do anything at all for the present queries. There. Accuse me of practising Cargo Cult if you want.

Anyway, the result is looking as awful as I had expected given my first impressions with January 1st, and clearly, ensuring birthdays after 1850 is not enough to filter out junk:
```
person=http://www.wikidata.org/entity/Q112689783
ddate=0080-01-01T00:00:00Z
bdate=1920-01-01T00:00:00Z
personName=Enrico Mezzasalma

person=http://www.wikidata.org/entity/Q19976926
ddate=1342-01-01T00:00:00Z
bdate=2000-01-01T00:00:00Z
personName=Peter Jonsson

person=http://www.wikidata.org/entity/Q19291026
ddate=1400-01-01T00:00:00Z
bdate=2000-01-01T00:00:00Z
personName=Galceran Marquet
...
```
It seems Wikidata even uses 2000-01-01 as some sort of NULL value. Dang. Let's filter out January 1st, then:
```
SELECT ?person ?personName ?bdate ?ddate
WHERE {
  ?person rdfs:label …
```
⎆

Falsche Dichotomien

12022:215:0 ( 2022-08-03)

Über den Köpfen von Demonstrierenden: Schneegestöber

So sieht Engagement für Freiheit und Emanzipation aus: Im Schneegestöber demonstrierten die Menschen im Februar 2018 gegen die Militärs und Kriegsherren, die sich in der Münchner Edelunterkunft Bayrischer Hof zu ihrer „Sicherheitskonferenz“ getroffen haben.

Seit dem Überfall auf die Ukraine grassiert das Aufziehen falscher Dichotomien (weniger elegant gesagt: sich angeblich ausschließender Alternativen) auch bei Menschen, die das vermutlich nicht im Rhetorikkurs gelernt haben und oft sogar guten Willens sind. Wer in den letzten Monaten normale Zeitungen oder Twitter gelesen hat, wird zumindest die folgenden Figuren gesehen haben (es gibt eine ganze Ecke mehr):

Entweder wir liefern Waffen oder wir unterstützen Angriffskriege (Quatsch: einfach mal selbst keine Angriffskriege und Drohnenballereien mehr machen und dann auf eine effektive Ächtung solcher Aktionen hinarbeiten wäre viel effektiver)
Entweder du bist für „uns“ oder du bist für Putin (Quatsch: Ich habe schon des Öfteren gegen Putin-Besuche demonstriert und bin dafür auch einmal im Auftrag von Olaf Scholz verprügelt worden; mensch kann prima gegen alle Sorten blutiger Hähne[1] sein)
Entweder lassen wir auf Russen schießen oder die Leute in der Ukraine werden alle getötet (Quatsch: Das russlandgefällige Janukowitsch-Regime war jetzt nicht klasse, aber ausweislich diverser Wahlen oder Leaks nicht qualitativ verschieden von den uns gefälligen Regimes von, sagen wir, Kutschma und Tymoschenko oder auch Poroschenko; es ist nach aller realistischen historischen Erfahrung völlig sicher, dass im Krieg viel mehr Menschen sterben und leiden werden als bei einem schnellen Regime Change, zumal wenn die regimechangenden Truppen dann nicht so ewig bleiben wie die unseren in Afghanistan und im Irak und/oder die Bevölkerung schnell aus dem Kriegsmodus herauskommt)
Entweder willst du Volk und Nation der Ukraine retten oder du willst die Leute in der Ukraine in Knechtschaft sehen (Quatsch: spätestens seit Brecht haben nette Menschen aufgehört, von „Volk“ zu reden, denn „Bevölkerung“ verhindert Fehlschlüsse, und spätestens seit dem 20. Jahrhundert sollte eigentlich Konsens bestehen, dass das mit den „Nationen“ eine eher bescheidene Idee war; mit der Verteidigung bzw. Erringung von Menschen- und Bürgerrechten haben Volk und Nation jedenfalls längst nichts mehr zu tun)
Entweder du schießt oder du tust gar nichts (Quatsch: Im Gegenteil ist eine geschichtliche Konstante, dass sozialer Fortschritt, der aus den Gewehrläufen kommt, nicht viel taugt und jedenfalls nicht lange anhält)

Es lohnt sich grundsätzlich, aber ganz besonders bei all den kriegseuphorischen Äußerungen, auf solche falschen Dichotomien zu achten. Wie gesagt: Nicht alle, die sowas verwenden, sind im Bereich finsterer Rhetorik unterwegs. Aber wer in diesem Bereich unterwegs ist, verwendet sie fast immer. Mal sehen, ob ich den Fleiß habe, mehr unter dem Tag Dichotomien zu schreiben, den ich anlässlich dieses Posts angelegt habe

Nachtrag (2023-04-01)

Nee, habe ich wieder weggemacht, weil ich den Fleiß noch nicht hatte.

Dennoch kann ich mich in der Kriegsfrage eigentlich nicht mehr groß über solche Tricks echauffieren, denn Kriegsbegeisterung hält erfahrungsgemäß selten lange an; ich bin eigentlich recht zuversichtlich, dass jedenfalls diejenigen neuen Fans der Panzerhaubitze, die noch etwas Herz und/oder Verstand haben, in recht absehbarer Zeit zu wieder etwas gewaltskeptischeren Positionen zurückkehren werden, ohne dass sich erst richtig viele Leute totschießen müssen.

Was allerdings taz-Chefreporter (was immer das sein mag) Peter Unfried in der taz vom Samstag gebracht hat, hat mich dann doch schlucken lassen:

Die Gewaltoption [konkreter weiter oben fomuliert: militärischer Massenmord] ist Voraussetzung einer freien und emanzipatorischen Zukunft.

Ob es nun sinnvoll ist oder nicht, ich musste dem widersprechen, und die taz hat meinen Leserbrief heute auch abgedruckt:

Peter Unfried will durch Militär eine freie und emanzipatorische Zukunft sichern. Das ist nicht nur absurd, ist doch der autoritäre Gewaltapparat Militär die Antithese zu Freiheit und Emanzipation. Es ist auch schlicht unhistorisch. Versammlungsfreiheit und Datenschutz, Wahlrecht und Atomausstieg, Streikrecht und straffreie Abtreibung, ganz besonders das Recht, nicht morden zu müssen, auch bekannt als Kriegsdienstverweigerung: Alles in der weiteren Umgebung von Freiheit haben Menschen ohne Militär – in Gewerkschaft, Blaustrümpfen oder Fridays for Future – gegen Menschen mit Militär – ihre Regierungen nämlich – erkämpft und tun es auch gerade jetzt überall Tag für Tag. Wenn Unfried hingegen seine Freiheit auf das Militär baut, hat er sie schon verloren.

[1]

Wer es nicht erkennt: Das bezieht sich auf ein sehr zeitgemäßes Lied der Brecht/Weill-Combo. Seit dem 24.8.2021 sind nun Brechts Werke endlich gemeinfrei, und so kann ich den mich immer wieder beeindruckenden Text bedenkenlos zitieren:

Am Grunde der Moldau wandern die Steine
Es liegen drei Kaiser begraben in Prag
Das Große bleibt groß nicht und klein nicht das Kleine
Die Nacht hat zwölf Stunden, dann kommt schon der Tag.

Es wechseln die Zeiten.  Die riesigen Pläne
Der Mächtigen kommen am Ende zum Halt.
Und gehn sie einher auch wie blutige Hähne
Es wechseln die Zeiten, da hilft kein Gewalt.

Am Grunde der Moldau wandern die Steine
Es liegen drei Kaiser begraben in Prag
Das Große bleibt groß nicht und klein nicht das Kleine
Die Nacht hat zwölf Stunden, dann kommt schon der Tag.

SPARQL 2: Improvising a client

12022:211:6 ( 2022-07-31)
There is still a lot of hair on the Yak I am shaving in this little series of posts on SPARQL. All the Yaks shown in the series lived on the Valüla Mountain in Vorarlberg, Austria.
This picks up my story on figuring out whether birthdays are dangerous using SPRAQL on Wikidata. You can probably skip this part if you're only interested in writing SPARQL queries to Wikidata and are happy with the browser form they give you. But you shouldn't. On both accounts.

At the end of part one, I, for one, was unhappy about the Javascript-based UI at Wikidata and had decided I wanted a user interface that would let me edit my queries in a proper editor (in particular, locally on my machine, giving me the freedom to choose my tooling).

My browser's web inspector quickly showed me that the non-Javascript web UI simply sent a query argument to https://query.wikidata.org/sparql. That's easy to do using curl, except I want to read the argument from a file (that is, the one I am editing in my vi). Helpfully, curl's man page informs on the --form option:

This enables uploading of binary files etc. To force the 'content' part to be a file, prefix the file name with an @ sign. To just get the content part from a file, prefix the file name with the symbol <. The difference between @ and < is then that @ makes a file get attached in the post as a file upload, while the < makes a text field and just get the contents for that text field from a file.
Uploads, Multipart, Urlencoded, Oh My!

In this case, Wikidata probably does not expect actual uploads in the query argument (and the form does not submit it in this way), so < it ought to be.

To try it, I put:
```
SELECT ?p ?o
WHERE {
  wd:Q937 ?p ?o.
}
LIMIT 5
```
(the query for everything Wikidata says about Albert Einstein, plus a LIMIT clause so I only pull five triples, both to reduce load on Wikidata and to reduce clutter in my terminal while experimenting) into a file einstein.rq. And then I typed:
```
curl --form query=<einstein.rq https://query.wikidata.org/sparql
```
into my shell. Soberingly, this gives:
```
Not writable.
```
Huh? I was not trying to write anything, was I? Well, who knows: Curl, in its man page, says that using --form does a POST with a media type of multipart/form-data, which many web components (mistakenly, I would argue) take as a file upload. Perhaps the remote machinery shares this misconception?

Going back to the source of https://query.wikidata.org/, it turns out the form there does a GET, and the query parameter hence does not get uploaded in a POST but rather appended to the URL. Appending to the URL isn't trivial with curl (I think), but curl's --data option at least POSTs the parameters in application/x-www-form-urlencoded, which is what browsers do when you don't have uploads. It can read from files, too, using @<filename>. Let's try that:
```
curl --data query=@einstein.rq https://query.wikidata.org/sparql
```
Oh bother. That returns a lenghty message with about a ton of Java traceback and an error message in its core:
```
org.openrdf.query.MalformedQueryException: Encountered " <LANGTAG> "@einstein "" at line 1, column 1.
Was expecting one of:
    "base" ...
    "prefix" ...
    "select" ...
    "construct" ...
    "describe" ...
    "ask" ...
```
Hu? Apparently, my query was malformed? Helpfully, Wikidata says what query it saw: queryStr=@einstein.rq. So, curl did not make good on its promise of putting in the contents of einstein.rq. Reading the man page again, this time properly, I have to admit I should have expected that: “if you start the data with the letter @“, it says there (emphasis mine). But haven't I regularly put in query parameters in this way in the past?

Sure I did, but I was using the --data-urlencode option, which is what actually simulates a browser and has a slightly different syntax again:
```
curl --data-urlencode query@einstein.rq https://query.wikidata.org/sparql
```
Ha! That does the trick. What comes back is a bunch of XML, starting with:
```
<sparql xmlns='http://www.w3.org/2005/sparql-results#'>
  <head>
    <variable name='p'/>
    <variable name='o'/>
  </head>
  <results>
    <result>
      <binding name='p'>
        <uri>http://schema.org/version</uri>
      </binding>
      <binding name='o'>
        <literal datatype='http://www.w3.org/2001/XMLSchema#integer'>1692345626</literal>
      </binding>
    </result>
```
Making the Output Friendlier: Turtle?

Hm. That's not nice to read. I thought: Well, there's Turtle, a nice way to write RDF triples in plain text. In RDF land, people rather regularly support the HTTP accept header, a wildly underused and cool feature of HTTP that lets a client say what kind of data it would like to get (see Content negotiation in the Wikipedia). So, I thought, perhaps I can tell Wikidata to produce Turtle using accept?

This plan looks like this when translated to curl:
```
curl --header "accept: text/turtle" \
  --data-urlencode query@einstein.rq https://query.wikidata.org/sparql
```
Only, the output does not change, Wikidata ignores my request.

Thinking again, it is well advised to do so (except it could have produced a 406 Not Acceptable response, but that would probably be even less useful). The most important thing to remember from part one is that RDF talks about triples of subject, predicate, and object. In SPARQL, you have a SELECT clause, which means a result row in general will not consist of subject, predicate, and object. Hence, the service couldn't possibly return results in Turtle: What does not consist of RDF triples canot be serialised as RDF triples.
Making the Output Friendlier: XSLT!

But then what do I do instead to improve result readability? For quick and (relatively) easy XML manipulation on the command line, I almost always recommend xmlstarlet. While I give you its man page has ample room for improvement, and compared to writing XSL stylesheets, the command line options of xmlstarlet sel (use its -h option for explanations) are somewhat obscure, but it just works and is compact.

If you inspect the response from Wikidata, you will notice that the results come in result elements, which for every variable in your SELECT clause have one binding element, which in turn has a name attribute and then some sort of value in its content; for now, I'll settle for fetching either uri or literal (again, part one has a bit more on what that might mean). What I need to tell xmlstarlet thus is: “Look for all result elements and produce one output record per such element. Within each, make a name/value pair from a binding's name attribute and any uri or literal element you find.” In code, I furthermore need to add an XML prefix definition (that's totally orthogonal to RDF prefixes). With the original curl and a pipe, this results in:
```
curl --data-urlencode query@einstein.rq https://query.wikidata.org/sparql \
| xmlstarlet sel -T -N s="http://www.w3.org/2005/sparql-results#" -t \
  -m //s:result --nl -m s:binding -v @name -o = -v s:uri -v s:literal --nl
```
Phewy. I told you xmlstarlet sel had a bit of an obscure command line. I certainy don't want to type that every time I run a query. Saving keystrokes that are largely constant across multiple command invocations is what shell aliases are for, or, because this one would be a bit long and fiddly, shell functions. Hence, I put the following into my ~/.aliases (which is being read by the shell in most distributions, I think; in case of doubt, ~/.bashrc would work whenever you use bash):
```
function wdq() {
  curl -s --data-urlencode "query@$1" https://query.wikidata.org/sparql
  | xmlstarlet sel -T -N s="http://www.w3.org/2005/sparql-results#" -t \
    -m //s:result --nl -m s:binding -v @name -o = -v s:uri -v s:literal --nl
}
```
(notice the $1 instead of the constant file name here). With an exec bash – my preferred way to get a shell to reflecting the current startup scripts –, I can now type:
```
wdq einstein.rq | less
```
and get a nicely paged output like:
```
p=http://schema.org/version
o=1692345626

p=http://schema.org/dateModified
o=2022-07-31T01:52:04Z

p=http://schema.org/description
o=ލިޔުންތެރިއެއް

p=http://schema.org/description
o=ಗಣಿತಜ್ಞ

p=http://schema.org/description
o=भौतिकशास्त्रातील नोबेल पारितोषिकविजेता शास्त्रज्ञ.
```
We will look at how to filter out descriptions in languagues one can't read, let alone speak, in the next instalment.

For now, I'm reasonably happy with this, except of course I'll get many queries wrong initially, and then Wikidata does not return XML at all. In that case, xmlstarlet produces nothing but an unhelpful error message of its own, because it …
⎆
SPARQL and Wikidata 1: Setting out

12022:208:1 ( 2022-07-27)
If you continue, you will read about a first-rate example of Yak Shaving
While listening to a short biography of the astrophysicist Mary Lea Heger (my story; sorry, in German), I learned that she died on her birthday. That made me wonder: How common is that? Are people prone to die on their birthdays, perhaps because the parties are so strenuous, perhaps because they consider them a landmark that they are so determined to reach that they hold on to dear life until they have reached it? Or are they perhaps less likely to die because all that attention strengthens their spirits?

I figured that could be a nice question for Wikidata, a semantic database that feeds Wikipedia with all kinds of semi-linguistic or numeric information. Even if you are not Wikipedia, you can run fairly complex queries against it using a language called SPARQL. I've always wanted to play with that, in particular because SPARQL seems an interesting piece of tech. Answering the question of the letality of birthdays turned out to be a mildly exciting (in a somewhat nerdy sense) journey, and I thought my story of how I did my first steps with SPARQL might be suitably entertaining.

Since it is a relatively long story, I will split it up into a few instalments. This first part relates a few preliminaries and then does the first few (and very simple) queries. The preliminaries are mainly introducing the design of (parts of) RDF with my take on why people built it like that.
Basics: RDF in a few paragraphs

For motivating the Resource Description Format RDF and why people bother with it, I couldn't possibly do better than Norman Gray in his witty piece on Jordan, Jordan and Jordan. For immediate applicability, Wikidata's User Manual is hard to beat.

But if you're in a hurry, you can get by with remembering that within RDF, information is represented in triples of (subject, predicate, object). This is somewhat reminiscent of a natural-language sentence, although the “predicate“ typically would be a full verb phrase, possibly with a few prepositions sprinkled in for good measure. Things typically serving as predicates are called “property“ in RDF land, and the first example for those defined in wikidata, P10 [1], would be something like has-a-video-about-it-at or so, as in:
```
"Christer Fuglesang", P10, http://commons.wikimedia.org/wiki/Special:FilePath/Christer%20Fuglesang%20en.webm
"Christer Fuglesang", P10, http://commons.wikimedia.org/wiki/Special:FilePath/Christer%20Fuglesang%20ru.webm
```
If you know about first order logic: It's that kind of predicate. And please don't ask who Christer Fuglesang is, the triples just came up first in a query you will learn about a bit further down.

This was a bit of a simplification, because RDF will not usually refer to a thing (an “entity“ in RDF jargon) with a string (“literal”), if only because there could be multiple Christer Fuglesangs and a computer would be at a loss as to which one I mean in the two triples above. RDF instead talks about “resources“, which is anything that has a URI and encompasses both entities and properties. So, a statement as above would actually combine three URIs:

http://www.wikidata.org/entity/Q317382, http://www.wikidata.org/prop/direct/P10, http://commons.wikimedia.org/wiki/Special:FilePath/Christer%20Fuglesang%20en.webm
CURIEs

That is a lot of stuff to type, and thus almost everything in the RDF world supports URL abbreviation using prefixes. Basically, in some way you say that whenever there's wpt: in a token, some magic replaces it by http://www.wikidata.org/prop/direct/. Ff you know about XML namespaces (and if you're doing any sort of non-trivial XML, you should): same thing, except that the exact syntax for writing down the mapping from prefixes to URIs depends on how you represent the RDF triples.

These “words with a colon that expand to long URIs by some find-and-replace rules“ were called CURIEs, compact URIs, for a while, but I think that term has become unpopular again. I consider this a bit of a pity, because it was nice to have a name for them, and such a physics-related one on top. But it seems nobody cared enough to push the W3C draft for that ahead.

As with XML namespaces, each RDF document could use its own prefix mapping; if you want, you could instruct an RDF processor to let you write wikidata-direct-property: for http://www.wikidata.org/prop/direct/ rather than wpt: as usual. But that would be an unfriendly act. At least for the more popular collections of RDF resources, there are canonical prefixes: you don't have to use them, but everyone will hate you if you don't. In particular, don't bind well-known prefixes like foaf: (see below) to URIs other than the canonical ones except when seeing whether a piece of software does it right or setting traps for unsuspecting people you don't like.

Then again, for what we are doing here, you do not need to bother about prefix mappings at all, because the wikidata engine has all prefixes we will use prefined and built in. So, as long as you are aware that you can replace the funny prefixes with URI parts and that there is some place where those URIs parts are defined, you are fine.

Long URIs in RDF?

You could certainly ask why we're bothering with the URIs in the first place if people in practice use the canonical prefixes almost exclusively. I think the main reason RDF was built on URIs was because its parents on the one hand wanted to let everyone “build” resources with minimal effort. On the other hand, they wanted to ensure as best they could that two people would not accidentally use the same resource identifier while meaning different things.

To ensure the uniqueness of identifiers, piggybacking on the domain name system, which already makes sure that there are never two machines called, say, blog.tfiu.de in the world, is a rather obvious move. In HTTP URIs, domain names show up as the authority (the host part, the thing between the first colon and the double slash), and so with URIs of that sort you can start creating (if you will) your resources and would never conflict with anyone else as long as hold on to your domain.

In addition, nobody can predict which of these namespace URIs will become popular enough to warrant a globally reserved prefix of their own; you see, family-safe prefixes with four (or fewer) letters are a rather scarce resource, and you don't want to run a registry of those. If you did, you would become really unpopular with all the people you had to tell things like “no, your stuff is too unimportant for a nice abbreviation, but you can have aegh7Eba-veeHeql1:“

The admittedly unwieldy URIs in practice also have a big advantage, and one that would require some complex scheme like the Handle system if you wanted to replicate it with prefixes: most of the time, you can resolve them.
Non-speaking URIs

While RDF itself does not care, most URIs in this business actually resolve to something that is readable in a common web browser; you can always try it with the resources I will be mentioning later. This easy resolution is particularly important in the case of Wikidata's URIs, which are essentially just numbers. Except for a few cases (wd:Q42 is Douglas Adams, and wd:Q1 is the Universe), these numbers don't tell you anything.

There is no fixed rule that RDF URIs must have a lexical form that does not suggest their meaning. As a counterexample, http://xmlns.com/foaf/0.1/birthday is a property linking a person with its, well, birthday in a popular collection of RDF resources[2] called foaf (as in friend of a friend – basically, you can write RDF-complicant address books with that).

There are three arguments I have heard against URIs with such a speaking form:
- Don't favour English (a goal that the very multilingual Wikipedia projects might plausibly have).
- It's hard to automatically generate such URIs (which certainly is an important point when someone generates resources as quickly and with minimal supervision as Wikidata).
- People endlessly quarrel about what should be in the URI when they should really be quarrelling about the label, i.e., what is actually shown to readers in the various natural languages, and still more about the actual concepts and definitions. Also, you can't repair the URI if you later find you got the lexical form slightly wrong, whereas it's easy to fix labels.
I'm not sure which of these made Wikidata choose their schema of Q<number> (for entities) and P<number> (for properties) – but all of them would apply, so that's what we have: without looking …
⎆
Strafgericht ist für die anderen

12022:206:1 ( 2022-07-25)

Als vor ein paar Wochen der der Olivindex tief im braunen Bereich war, war allenthalben der Wunsch zu hören, Wladimir Putin möge sich möglichst schnell vor dem Internationalen Strafgerichtshof verantworten. Daraus wird wohl schon deshalb nichts, weil Russland das Gericht nicht anerkennt.

Das aber fanden die RuferInnen nach Gerechtigkeit damals in der Regel ebenso wenig erwähnenswert wie die Tatsache, dass auch die USA die Jurisdiktion des Haager Gerichtshofs ebensowenig anerkennen wie unsere Regierung beispielsweise das Verbot von Atombomben. „It wouldn't do to mention,“ sagt mensch da im englischen Sprachraum, zumal es bei der US-Abstinenz genau um Straffreiheit bei Handlungen in Angriffskriegen („Kriegsverbrechen“ halte ich ja für einen Pleonasmus) geht.

Wer aber glaubt, die EU verhalte sich nennenswert anders, täuscht sich. Gerade jetzt gibt es dazu höchst aufschlussreiches Anschauungsmaterial. Die EU rüstet nämlich den Apparat im Senegal nicht nur mit fieser Biometrie auf, sie will dort mit Frontex auch selbst aktiv werden. Die Bedingungen dazu werden gerade verhandelt. Zum Glück ist der EU-Apparat voll undichter Stellen, und so konnte Statewatch jüngst die Verhandlungsposition der Kommission befreien.

Und darin wird blank gezogen:

[Frontex-Leute] sollten berechtigt sein, alle Aufgaben der Grenzkontrolle zu erfüllen und die dazu nötige Exekutivgewalt ausüben [...]; sie sollten berechtigt sein, Dienstwaffen, Munition und Ausrüstung mitzuführen und diese gemäß der Gesetze der Republik Senegal zu nutzen.

Original

Team members should be entitled to perform all the tasks and exercise all the executive powers required for border control (border checks and border surveillance within the meaning of Regulation (EU) 2019/18962); they should be entitled to carry service weapons, ammunition and equipment and use them in accordance with the laws of the Republic of Senegal.

(Übersetzung von mir; die offizielle EU-Übersetzung ist nicht befreit).

Mit anderen Worten: Die EU wird den Senegal zur Übergabe seiner staatlichen Gewalt zwingen. Wer sich fragt, was passiert, wenn sich der Senegal nicht darauf einlässt, mag sich die Geschichte der jüngsten Erpressung von Kenia durch die EU ansehen, als sich das Land gegen EU-Dumpingimporte (von der EU euphemistisch als „European Partnership Agreement“ bezeichnet) wehren wollte.

Und wer meint, der Senegal dürfte vielleicht nicht die Exekutive, aber doch die Legislative behalten, wird im nächsten Absatz eines Besseren belehrt:

Insbesondere sollten [die Frontex-Leute] unter allen Umständen volle Immunität gegenüber der Strafjustiz der Republik Senegal genießen. Sie sollten ebenfalls zivilrechtliche Immunität für Handlungen genießen, die sie in Wahrnehmung ihrer offiziellen Funktionen vornehmen.

Original

In particular, these staff should enjoy full immunity from the criminal jurisdiction of the Republic of Senegal under all circumstances. They should also enjoy immunity from civil jurisdiction of the Republic of Senegal for the acts performed by them in the exercise of their official functions.

Sind wir mal besser froh, dass niemand irgendwem im Senegal Panzerhaubitzen liefert. Slava Senegal!

⎆
Mary Lea Heger: Interstellares Natrium und Geburtstage

12022:204:6 ( 2022-07-24)
Der Stern δ Orionis in einer Aufnahme von 1927 (B5232a aus HDAP) – das war eines der zwei Objekte, in deren Spektrum Mary Lea Heger das interstellare Natrium entdeckt hat.[1]
In der DLF-Sternzeit vom 13. Juli ging es um Mary Lea Heger, die vor rund 100 Jahren entdeckte, dass es Natrium im Raum zwischen den Sternen gibt (auch wenn sie sich im verlinkten Artikel von 1919 noch nicht ganz sicher war, wo genau). Wer mal Himmelsaufnahmen aus der Zeit gesehen hat, wird ahnen, wie haarig das gewesen sein muss.

Heger hat nämlich Spektren aufgenommen, was damals überhaupt nur für sehr helle Sterne wie den oben abgebildeten δ Orionis alias Mintaka (der am weitesten rechts stehende Gürtelstern des Orion) sinnvoll ging. Aus diesen Spektren hat sie dann Radialgeschwindigkeiten abgeleitet, also im Groben beobachtete Wellenlängen von Spektrallinien bekannter Elemente mit deren auf der Erde messbaren Wellenlängen verglichen, daraus die Blau- bzw. Rotverschiebung abgeleitet und daraus wiederum bestimmt, wie schnell sich die Objekte gerade auf uns zu oder von uns weg bewegen.

Ehrlich gesagt weiß ich gar nicht, wie das damals gemacht wurde. Heute malt einem der Computer schöne Kurven und kann dann auch beliebige Funktionen dranfitten. Damals hingegen war, denke ich, schon die numerische Erfassung der Schwärzungen der Fotoplatte (bei der ihrerseits doppelte Schwärzung mitnichten doppeltes Licht bedeutet) eine echte Herausforderung. Die Wikipedia schreibt leider unter Densitometer nichts zur Geschichte dieser Geräte, und zu einer richtigen Recherche kann ich mich gerade nicht aufraffen.

Mintaka und Hegers zweites Objekt, der von uns aus kaum ordentlich zu beobachtende β Scorpii alias Akrab[2], sind beides ziemlich heiße Sterne, im Jargon Spektralklasse B mit Oberflächentemperaturen deutlich über 20000 Kelvin (die Sonne: 6000 K). Weil bei diesen Temperaturen die Atome recht schnell unterwegs sind, wenn sie Photonen absorbieren, sind die Linien solcher Sterne in der Regel breit (vgl. Dopplerverbreiterung); auf den Fotos, aus denen solche Spektren gewonnen wurden, wirken die Linien sozusagen ausgewaschen.

Tanzende und stehende Linien

Heger hat nun aber auch ein paar recht scharfe Linien von Kalzium und Natrium in den Spektren dieser Sterne gefunden, und zwar in Absorption, was heißt: Irgendwo zwischen da, wo das Licht herkommt und Hegers Spektrographen muss es Kalizum- und Natriumatome geben, die das Licht der passenden Wellenlängen absorbiert (und dann wieder woandershin emittiert) haben. Und davon nicht zu knapp.

Ein modernes Spektrum von β Ori (vom FEROS-Spektrographen der ESO, HD36485_1069462_2014-08-24T08:30:43.517_S0.5x11_1x1_UVB_NOD). Auf der x-Achse ist die Wellenlänge in Nanometer, auf der y-Achse die Flussdichte in Instrumenteneinheiten. Gezeigt ist die Umgebung der Fraunhofer-Linien H (Labor: 393,368 nm) und K (Labor: 396,847 nm) des einfach ionisierten Kalziums. Links ist eine relativ schmale und unstrukturierte Linie zu sehen, wie sie Heger für die interstellare Absorption gesehen haben wird, rechts dann eine breite Linie mit vielen Komponenten von den Einzelsternen: die Höcker da drauf würden tanzen, wenn mensch einen Film machen würde. Nach etwas Überlegung habe ich beschlossen, mich nicht festzulegen, was welche Linie ist…

Sowohl Akrab als auch Mintaka sind zudem recht enge Doppelsterne[3]. So enge, dass sie mit damaligen Techniken wie ein Stern erschienen. Dass es sich um Doppelsterne handelt, war bekannt, weil in ihren Spektren (im Groben) jede Linie nicht ein Mal, sondern zwei Mal vorhanden ist, und die Teile eines Paars darüber hinaus regelmäßig umeinander tanzen. Die Erklärung: jeder Stern macht für sich eine Linie, die je nach Stellung in der Bahn anders dopplerverschoben ist als die seines Partners. Nun sind solche Sterne sehr schwer, und sie umkreisen sich auf relativ engen Bahnen (bei Mintaka: das Jahr ist im engen Paar 5.7 Tage lang), so dass die Bahngeschwindigkeiten bis hunderte Kilometer pro Sekunde betragen können[4]. Damit sind auch die Dopplerverschiebungen der Linien recht ernsthaft, und so ist die Natur der ersten dieser spektroskopischen Doppelsterne schon Ende des 19. Jahrhunderts aufgefallen.

Nur: Hegers scharfe Linien tanzen nicht. Sie bleiben stur stehen, während die Sterne umeinander rasen. Und damit ist klar, dass die absorbierenden Atome zumindest nicht zu den einzelnen Sternen gehören. Sie könnten im Prinzip aus der Erdatmosphäre kommen, denn die Natriumschicht in so um die 100 km Höhe, die heute für Laser-Leitsterne verwendet wird, ist in hinreichend empfindlichen Spektren durchaus zu sehen. Wie das mit damaligen Spektren war, weiß ich nicht, die Schicht als solche wurde aber erst 1929 entdeckt (was sich jedoch nur auf die spezifische Verteilung des Natriums beziehen mag – andererseits ist neutrales Natrium in Gegenwart von Sauerstoff nicht gerade stabil. Also: ich weiß es wirklich nicht).

Abgeleitete Kopfzahl: mit 30⋅3600 Sachen um die Sonne

Heger wird aber (auch wenn sie das im verlinkten Artikel nicht schreibt, weil die entsprechende Korrektur Teil der Standard-Datenreduktion war und ist) in ihren scharfen Linien doch eine Bewegung gesehen haben, nämlich um etwas weniger als 30 km ⁄ s. Das ist der Reflex der Bewegung der Erde um die Sonne, und der wäre in atmosphärischen Linien nicht zu sehen, da sich ja die Atmosphäre mit der Erde bewegt.

Die Geschwindigkeit der Erde bei ihrem Weg um die Sonne ist übrigens mit zwei Kopfzahlen schnell abgeschätzt: erstens dem Dauerbrenner 30 Millionen Sekunden pro Jahr (oder π⋅10⁷ s, was tatsächlich die Art ist, in der ich mir das merke) und dann die 150 Millionen km (was ich mir als 1.5⋅10¹¹ m merke) für den Radius der Erdbahn. Die Geschwindigkeit ist dann einfach Umfang der Erdbahn geteilt durch ein Jahr oder in überschaubareren Einheiten

(2⋅π⋅1.5⋅10⁸ km)/(π⋅10⁷ s) = 3⋅10¹ km ⁄ s

Das “etwas weniger“ als diese 30 km ⁄ s kommt daher, dass die volle Amplitude dieser Bewegung nur bei Sternen in der Ekliptik, also der Abbildung der Erdbahn am Himmel, zu sehen ist. Geht mensch von dieser gedachten Linie weg, wird die Geschwindigkeitskomponente in Richtung des Sterns kleiner (nämlich mit dem Kosinus der ekliptikalen Breite), bis am ekliptikalen Pol gar kein Reflex der Erdbewegung mehr zu sehen ist[5].

Akrab nun steht in einem Tierkreiszeichen und von daher quasi per definitionem nahe an der Ekliptik. Auch der Orion (gleich südlich vom Stier) ist nicht weit von ihr entfernt – die ekliptikale Breite von Mintaka ist ungefähr 23.5 Grad. Deshalb taugt 30 km ⁄ s schon als Abschätzung für die Amplitude der Radialgeschwindigkeit der beiden Sterne aufgrund der Bewegung der Erde um die Sonne.

Mit 10⋅3600 Sachen mit der Sonne durch die Strom

Tatsächlich konnte Mary Lea Heger die Rotverschiebungen ihrer scharfen Linien und unscharfen Linien messen und kam auf folgendes Geschwindigkeiten (alles in km/s):

Objekt β Sco δ Ori

Natrium -9.2 17.6

Kalzium -8.5 18.7

RG des Systems -11.0 15.2

Sonnenbewegung -10.7 18.1

Die „Sonnenbewegung“ ist dabei das, was damals schon gemessen war als Bewegung der Sonne gegenüber der allgemeinen galaktischen Rotation von etwa 200 km ⁄ s – wie die damals darauf gekommen sind, ist eine ganz eigene Geschichte –, projiziert auf den Richtungsvektor zum jeweiligen Stern. Die „Radialgeschwindigkeit (RG) des Systems“ hingegen ist die Geschwindigkeit, mit der der Schwerpunkt der jeweiligen Sternsysteme auf uns zukommt oder sich von uns entfernt.

Dass die Sonnenbewegung und Radialgeschwindigkeiten hier recht eng beieinander liegen, ist übrigens kein Zufall. Beide Sterne sind wie gesagt heiße B-Sterne, und diese sind[6] nach astronomischen Maßstäben sehr jung, gerade erst (also: vor ein paar oder ein paar zehn Millionen Jahren) aus Gaswolken geboren. Die Gaswolken wiederum laufen sehr brav mit der allgemeinen galaktischen Rotation mit. Sie können gar nicht anders, denn anders als die Sterne kollidieren Gaswolken in Galaxien durchaus miteinander, wenn eine versucht, quer zum Strom zu schwimmen. Wenn sie dann kollidieren, verlieren sie rasch ihre Eigengeschwindigkeiten (und produzieren sehr wahrscheinlich noch eifrig Sterne). Was übrig bleibt, läuft wieder brav mit dem Rest der Galaxis.

Sterne hingegen können sich frei durch die Galaxis bewegen, weil sie praktisch nie mit anderen Sternen kollidieren – für einen Stern, kompakt wie er ist, ist die Galaxis quasi ein Vakuum, wenn auch eins mit Gavitationsfeld. Gerät ein Stern allerdings in die Nähe schwerer Dinge (wie etwa solchej Wolken), wird er ein wenig aus seiner Bahn gehoben, und das äußert sich am Ende in Eigengeschwindigkeiten wie der Sonnenbewegung von oben. Junge Sterne hatten noch keine Zeit, diese Sorte Schwung zu holen, und so ist die Radialgeschwindigkeit oben eigentlich nichts anderes als die Sonnenbewegung.

Auch wenn Heger keine Fehlerschätzungen angibt, ist die Übereinstimmung der Geschwindigkeiten der scharfen Linien und der Sonnenbewegung umwerfend gut, jedenfalls, wenn mensch die Schwierigkeiten der in diese Tabelle eingehenden Messungen bedenkt. Tatsächlich gibt die Wikipedia für die Radialgeschwindigkeit des Gesamtsystems Akrab − 1±2 km ⁄ s gegen Hegers -11; in einem System aus sechs Sternen muss das noch nicht mal auf ein Problem bei Heger hindeuten, aber ganz ehrlich: Ich wäre sehr verwundert, wenn sie besser als auf, sagen wir, 5 km/s hätte messen können.

Hegers Fazit

Entsprechend war Heger in ihren Schlussfolgerungen vorsichtig:

The agreement of the velocity obtained from the D lines …
⎆
Wird Bolsonaro Schuld sein an der nächsten großen Seuche?

12022:201:2 ( 2022-07-20)
Wie verschiedene Metriken die Häufigkeit von Zoonosen beeinflussen: Abbildung zwei aus doi:10.1126/sciadv.abo5774. CC-BY-NC Winck et al.
Auch wenn (oder gerade weil) in China ein SARS-Erreger schon mal aus enem Labor entkommen ist, glaube ich ja immer noch ziemlich fest daran, dass SARS-2 aus (zu) engem Kontakt von Menschen und Wildtieren entstanden ist. Wo es viele Tiere gibt, sind solche Krankheiten mit tierischer Beteiligung, Zoonosen, Regel eher als Ausnahme, und wo es viele verschiedene Tiere gibt, ist entsprechend mit vielen Überraschungen zu rechnen. So erscheint Brasilien als ideales Land, um quantitative Schätzungen zu bekommen zur Frage, wie insbesondere neuartige Krankheitserreger Artgrenzen überwinden können und was dann passiert.

Das war das Projekt von Gisele R. Winck und Ciclilia Andreazzi vom Institiuto Oswaldo Cruz in Rio de Janeiro sowie KollegInnen von verschiedenen anderen brasilianischen Instituten, über das sie in „Socioecological vulnerability and the risk of zoonotic disease emergence in Brazil”, Science Advances 8 (2022), doi:10.1126/sciadv.abo5774, berichten – und auch gleich anmerken, dass Brasilien vielleicht doch kein ganz ideales Land ist, ist doch ein Großteil der derzeit in Brasilien grassierenden Zoonosen gar nicht in Amerika entstanden: Malaria, Dengue, Zika oder Gelbfieber kommen alle aus der alten Welt.

Aber es gibt auch Beispiele für Zoonosen aus Südamerika, so etwa Chagas, ein von Trypanosomen – das sind einzellige Eukaryoten, also in gewissem Sinn einfache Tiere – hervorgerufenes Syndrom, das zu tödlichen Verdauungsstörungen führen kann, sich aber nur gemeinsam mit relativ memmigen Wanzen weiterverbreiten kann.
Pfadanalyse

Winck et al versuchen, der Frage nach künftigen Zoonose-Risiken mit einer Pfadanalyse auf den Grund zu gehen, einer statistischen Methode zur Aufklärung von Netzwerken einander beeinflussender Größen, von der der ich, soweit ich mich erinnere, zuvor noch nie gehört habe. Diese Lücke dürfte wohl damit zusammenhängen, dass die Methode in der Biologie entwickelt wurde (ihr Erfinder war Populationsgenetiker) und im Bereich von Physik und Astronomie wenige etwas damit anzufangen wussten.

Eine entsprechende ADS-Anfrage (und das ADS hat eigentlich alles, was es in der Astronomie gibt) liefert dann auch vor allem Kram aus Randbereichen, darunter eine Studie in den Geophysical Review Letters, die fast in das aktuelle Thema passt: „Urban Vegetation Slows Down the Spread of Coronavirus Disease (COVID-19) in the United States“. Da allerdings wette ich ungelesen, dass von dem Effekt wenig übrigbleibt, wenn mensch die Korrelation zwischen graueren Vierteln und Armut auf der einen und SARS-2 und Armut auf der anderen Seite rausrechnet.

Wie dem auch sei: Bei einer Pfadanalyse braucht es eine Zielgröße (also das, dessen Verhalten erklärt werden soll) und „Kausalfaktoren“ (also Größen, das Verhalten der Zielgröße erklären sollen). Die Zielgröße im Paper ist die Fallzahl von einigen Zoonosen[1] in den verschiedenen brasilianischen Bundesstaaten.

Das grobe Modell, das der Arbeit zugrundeliegt, ist nun, dass enge Kontakte zwischen Menschen und Tieren, gerade wenn wie beim Verzehr von Bushmeat Blut im Spiel ist, die Zoonosen nach oben treibt. Es könnte auch indirekte Effekte geben, wenn es etwa Wildtieren schlechter geht, weil die Menschen gerade ihr Habitat zerstören, und daher Pathogene, die vorher selten und harmlos waren, genau dann durch die geschwächte Population rauschen, wenn Menschen und Wildtiere während der Rodungen und vor der Etablierung funktionierender Landwirtschaft besonders wahrscheinlich interagieren. Mit solchen Motivationen betrachtet die Arbeit folgende Kausalfaktoren (vgl. Tabelle 1 im Paper):
- Exposition gegenüber Zoonosen (Wie viele wilde Tiere gibt es? Wie gut ist die medizinische Versorgung der Nutztiere? Wie viel Boden ist (artenarme und in der Hinsicht wahrscheinlich eher sichere) landwirtschaftliche Fläche? Wie ist der Anteil der im Wesentlichen unberührten Fläche? Wie schnell gehen unberührte Flächen verloren?)
- Empfindlichkeit gegenüber Zoonosen (Bäume in Städten als Proxy für die Art der Besiedlung; Kontakt mit Hausmüll als Proxy für die Dichte des Kontakts zu Vektoren wie Ratten und Mücken; Zustand der Abwassererfassung; Bruttoinlandsprodukt pro EinwohnerIn als Proxy für die Armutsrate)
- Resilienz (Wie viel Gesundheitspersonal gibt es? In wie vielen Einrichtungen? Wie weit ist es in die nächste Stadt, in der spezialisierte Kliniken verfügbar sein werden?)
Ich muss an der Stelle ein wenig die Nase rümpfen, denn an sich kann dieses Modell nicht so richtig das, was die AutorInnen zu versprechen scheinen: Aufklären, was mensch tun könnte, um neue Zoonosen im Zaum zu halten. Die Zielgröße ist ja die Ausbreitung längst an den Menschen gewöhnter Erreger. Zudem wird die Mehrheit der untersuchten Zoonosen von einzelligen Tieren verursacht und nicht von Viren oder Bakterien, deren pandemisches Potenzial ich weit höher einschätze, zumal, wenn sie anders als die meisten Einzeller keine Zwischenwirte brauchen.

Aber seis drum: Ganz unplausibel ist ja nicht, dass, wo bekannte Erreger besonders intensiv zwischen Menschen und Tieren ausgetauscht werden, sich auch unbekannte Erreger allmählich an Menschen gewöhnen können.
BIP ist wurst

Angesichts des betrachteten Reichtums an Faktoren ist schon erstaunlich, dass die Mathematik der Pfadanalyse mit den Daten von Winck et al das Bild am Anfang des Posts ergibt (nicht signifikante Kausalfaktoren sind dort nicht gezeigt), also etwa das Bruttoinlandsprodukt pro EinwohnerIn keinen signifikanten Einfluss auf die Zoonoserate hat (was aus meiner Sicht nur heißen kann, dass es in Brasilien kein nützliches Maß für den Wohlstand mehr ist). In den Worten des Artikels:

Zoonotic epidemic risks, as inferred from the observed mean number of ZD cases, are positively associated with vegetation loss (path analysis coefficient = 0.30), mammalian richness (0.47), and remoteness (0.72) and negatively related to urban afforestation (−0.33) and vegetation cover (−0.82).

Also: Bäume in der Stadt (hätte ich erstmal nicht als einen wichtigen Faktor geraten, aber siehe das oben erwähnte GeoRL-Paper) und vor allem intakte Wildnis sind gut gegen Zoonosen. Eine hohe Dichte wilder Säugetiere, mit denen Menschen im Zuge von Entwaldung eifrig interagieren und, noch stärker, die Entfernung von größeren menschlichen Ansiedlungen befördern demgegegenüber solche Krankheiten.

Besonders stark ist dabei der Effekt der Bewaldung (bzw. Besteppung oder Bemoorung, wenn das die lokal vorherrschenden Ökosysteme sind): Sie fördert zwar sehr stark die Artenvielfalt von Säugetieren, doch hemmt sie dennoch Zoonosen insgesamt. Das passt erstaunlich gut zur Beobachtung von Jared Diamond in seinem lesenswerten Buch „Collapse: How societies choose to fail or succeed“[2], dass Entwaldung wohl der allerwichtigste Faktor für den Zusammenbruch von Zivilisationen ist.

Und dann die Schurken

Ich bin auf das Paper wie üblich über einen Beitrag in der DLF-Sendung Forschung aktuell gegekommen, in dem Fall vom 30.6. Darin wurde vor allem abgehoben auf den Schluss der AutorInnen, die aktuelle Herrschaft in Brasilien beeinflusse die Kausalfaktoren mit ihrer marktradikalen, reaktionären und teils auch anderweitig dummen Politik stark in Richtung Zoonose:

Ein weiterer wichtiger Aspekt, dessen Relevanz sich gerade erst erwiesen hat, ist die Empfindlichkeit gegenüber fehlgeleiteten politischen Maßnahmen, wie sie von den augenblicklichen Regierungen veranlasst wurden.

Original

Another important and recently experienced aspect is the vulnerability to misguided public policy actions made by current governments

Besonders gut hat mir dabei gefallen die Rede von einer „increasing socioecological degradation“, also einem zunehmenden sozio-ökologischen Verfall, zumal ich dabei an meine eigene brasilianische Geschichte denken musste.

Im Parco de Tijuca auf dem Stadtgebiet von Rio de Janeiro: Warnung vor den „Waldtieren“, die auf der Straße rumlaufen. Tatsächlich turnen Affen sogar durch die Telefonleitungen, die zum Nationalobservatorium führen.

Im Jahr 2014 habe ich rund eine Woche am Nationalobservatorium in Rio de Janeiro gearbeitet. Ich denke, es ist nicht verkehrt, so etwa in dieser Zeit den Höhepunkt der Wirkungen der Sozialpolitik von Lula da Silva zu verorten, der speziell mit seiner bolsa familia Dutzenden Millionen Menschen ein halbwegs menschenwürdiges Leben ermöglicht hat.

Das hatte sehr profunde Konsequenzen auch für Menschen aus der Mittelschicht. Mein Gastgeber etwa erzählte, er sei vor Lulas Sozialpolitik „Opfer ungefähr jedes Verbrechens gewesen, das es gibt“, und das sei eine recht typische Erfahrung der Cariocas gewesen. Demgegenüber sei in den vieleicht fünf Jahren vor meinem Besuch eigentlich nichts mehr in der Richtung passiert. Ein weiterer Kollege ergänzte, er sei in dieser Zeit nur einmal ausgeraubt worden, und zwar mit chirurgischer Präzision (seine Worte), als er in den frühen Morgenstunden schon ziemlich beschickert unterwegs gewesen sei und die Räuber die Nettigkeit hatten, ihm seinen Geldbeutel wieder zurückzugeben, zwar ohne Bargeld, aber mit allem Plastikwahnsinn, dessen Wiederbeschaffung wirklich viel Stress gewesen wäre.

Diese Zeiten sind lange vorbei. Nach dem (rückblickend ist diese Charakterisierung wohl nicht zu bestreiten) Putsch gegen Dilma ging die Politik zurück zur Umverteilung von unten nach oben, mit den erwartbaren Konsequenzen für das Leben in einer Stadt wie Rio – und den weniger offensichlichen Konsequenzen für das Heranbrüten der nächsten großen zoonotischen Pandemie.

Ich frage mich ja bei solchen Betrachtungen immer, wie Leute wie Bolsonaro eigentlich ruhig schlafen können. Aber dann: Die Frage stellt sich ja ganz analog für Scholz, Steinmeier, für Fischer und Schröder, die mit Hartz IV oder der versuchten Rentenprivatisierung ganz ähnliche Dinge, wenn auch vielleicht auf kleinerer Flamme, angerichtet haben. Und ich vermute, ich habe den Kern der Antwort schon berechnet: Allein der Umstand, dass diese Menschen Macht haben, macht es sehr wahrscheinlich, dass sie über erhebliche moralische Flexibilität verfügen.

[1] Im einzelnen Bilharziose, Leishmaniose (innere und Haut-; wird im Rahmen des Klimawandels auch in der BRD häufiger), Leptospirose (letzter großer Ausbruch in der …
⎆

Objekt	β Sco	δ Ori
Natrium	-9.2	17.6
Kalzium	-8.5	18.7
RG des Systems	-11.0	15.2
Sonnenbewegung	-10.7	18.1

Vorbildliches Friedrichstadt

12022:195:8 ( 2022-07-15)

Schwarzweißbild auf Tafel vor realen Häusern.

In Friedrichstadt zeigen Tafeln gerne Fotos von um die 1900, die oft genug bis in Details wie Fenstersprossen dem aktuellen Zustand entsprechen. Dieser Post ist ein vorsichtiger Lobpreis einer solchen Praxis.

Ich bin gerade im nordfriesischen Friedrichstadt, einem Städtchen nahe der Nordseeküste, das viele TouristInnen anzieht, vor allem wenn, wie jetzt gerade, das Wetter am Strand längere Aufenthalte dort eher unattraktiv macht. Diesen BesucherInnen wird Friedrichstadt gerne als „Stadt der Toleranz“ präsentiert. Angesichts einer jahrhundertelangen Präsenz pazifistischer und damit relativ sympathischer protestantischer Sekten wie der Mennoniten und Quäker ist das wahrscheinlich auch eine recht brauchbare Zuschreibung – gerade diese hatten mit weniger toleranten Obrigkeiten meist erhebliche Probleme.

Ich allerdings finde das Nest aus anderen Gründen bemerkenswert, und das nicht nur, weil die Toleranz Grenzen hatte, die zumindest halbwegs aufgeklärten Menschen völlig albern erscheinen: Die Unitarier mussten zum Beispiel wieder gehen, was um so erschütternder ist, als sich diese von der christlichen Rechtgläubigkeit vor allem in der Zurückweisung des wahrscheinlich durchgeknalltesten aller Dogmen unterscheiden, nämlich der Trinität.

Wir müssen uns Gott als Tafellappen vorstellen

Ich kann nicht widerstehen: Als ich in der Grundschule war, erzählte uns der Dorfpfarrer original, mensch müsse sich die dreifaltige Gottheit vorstellen wie einen Tafellappen. Er nahm daraufhin so einen und faltete ihn an fünf Stellen so, dass vorne drei Falten rausguckten. Ein Tafellappen, drei Falten. Wer andere aus seiner Stadt wirft, weil sie so einen offensichtlichen Polit-Kompromiss[1] nicht glauben wollen, verdient einen Toleranzpreis vielleicht doch nur eingeschränkt.

Nein, wirklich vorbildlich an Friedrichstadt ist die, trärä, Na… Na… na ja. Ich muss es ja doch irgendwann mal sagen: Nachhaltigkeit. Das Wort ist zwar inzwischen zu Heizmaterial für Dampfplauderer verkommen, aber an sich liegt es ja schon nahe, so leben zu wollen, dass das auch noch ein paar Jahrhunderte weitergehen kann. Die wichtigste Zutat dabei ist: Nicht (prozentual, also exponentiell) wachsen. Was um x% im Jahr wächst, verdoppelt sich nach ungefähr 75/x Jahren (oder so), und zehn Verdopplungszeiten entsprechen einer Vertausendfachung. Fast nichts auf dieser Welt kann sich vertausendfachen, ohne dass etwas gewaltig vor die Hunde geht.

Friedrichstadt hat sich dem Wachstum in mancherlei Hinsicht beeindruckend entzogen. Herzog Friedrich III von Gottorf hat den Ort in den 1620er Jahren als künftiges Handelszentrum mit ein paar tausend EinwohnerInnen planen lassen. Derzeit, 401 Jahre Jahre nach der Gründung, leben so um die 2500 Menschen hier. Um die Größenordnungen zu betonen: Wer 400 Jahre Zeit hat, hat auch bei einer Verdoppelungszeit von 40 Jahren noch eine Vertausendfachung, und 40 Jahre Verdoppelungszeit entsprechend weniger als zwei Prozent Jahreswachstum.

Fortzug in wirtschaftlich prosperierendere Gegenden

Friedrichstadt aber wuchs zumindest in der Bevölkerung nicht. Die entsprechende Statistik aus der Wikipedia sieht als Spline-geglätteter (was das Loch nach dem ersten Weltkrieg überbetont) Plot so aus:

Plot: Recht konstant bei 2500 verlaufende Linie mit einem jähen Anstieg in den 1940er Jahren und einem relativ steilen Rückgang danach.

Der Berg in den 1940er und 1950er Jahren ist Folge des Zuzugs von Geflüchteten vor allem aus den von der Sowjetunion eroberten bzw. später kontrollierten Gebieten. Sein Abschmelzen führen die Wikipedia-AutorInnen auf den „Fortzug der Vertriebenen in wirtschaftlich prosperierendere Gegenden“ zurück.

Auch wenn Bevölkerungsexport keine, hust, nachhaltige Strategie ist: Der Nettoeffekt ist eine konstante Bevölkerung, und bei recht maßvoller Entwicklung der Wohnfläche pro Mensch ist das auch im Stadtbild sichtbar, denn Friedrichstadt hat kaum Einfamilienhaus-Wüsten aus dem Auto-Zeitalter (auch wenn die Stadt, das Eingangsfoto zeigt es, der Automobilisierung nicht entgehen konnte).

Doch auch wirtschaftlich hat sich nicht allzu viel getan: Eine Mühle, die Kölln-Flocken hergestellt hat (na gut, vielleicht auch anderen Kram für die Firma), ist 2001 wegen mangelnder Kapazität geschlossen worden – wo sie stand, ist heute ein Komplex von Spiel- und Bolzplätzen. Andere Industrie hat schon vorher aufgegeben.

Und so lebt Friedrichstadt eben weitgehend von Tourismus. Es ist ja auch hübsch hier. Auch das würde ich jetzt nicht als „nachhaltig“ bezeichnen, zumal es ohne ein gewisses Niveau an industrieller Produktion nichts würde mit den fünf Stunden Lohnarbeit pro Woche. Aber dennoch ist es interessant, wie sich eine Stadt anfühlt, die 400 Jahre lang stagnierte, aus welchen Gründen und mit welchen Mitteln auch immer.

Ich muss sagen: Mir gefällt es in Friedrichstadt.

[1]

Ich persönlich vermute ja, dass es, als beim Konzil von Nicäa die Trinität beschlossen wurde, ähnlich zuging wie während der marktradikalen Hochschul„reformen“ der 1990er und Nullerjahre („Bologna-Prozess“), als jedeR jedeN aufs Kreuz zu legen versuchte und das Ergebnis völlig dysfunktionaler Quatsch ist.

Velorution Aber Hallo

12022:192:6 ( 2022-07-12)

Demo-Impressionen: Fahrrad mit Pappschild "Velorution jetzt", Fahrraddemo fährt auf eine Autobahnauffahrt

Weil mir mein Pappschild „Velorution Aber Hallo“ im Fridays-for-Future-Stil so gut gefiel (bis auf die Klettbänder war alles recyclet), muss ich kurz von der Demo für den Fahrradschnellweg zwischen Heidelberg und Mannheim erzählen.

Diese hat eine lange Tradition von inzwischen fast einem Jahrzehnt. Eine noch längere Tradition hat allerdings das Thema, nämlich (mindestens) eine Verbindung zwischen Heidelberg und Mannheim, auf der RadlerInnen nicht entweder ein einem Fort von rasenden Autos gequält werden oder im Übermaß Schnitzeljagd- und Querfeldein-Qualitäten benötigen. Seit größenordnungsmäßig 20 Jahren wird an dem Thema herumdiskutiert und -geplant, ohne dass etwas passiert wäre.

Um die Sache etwas in Bewegung zu halten, veranstalten ADFC und Co jedes Jahr im Juli eine Raddemo von Heidelberg nach Mannheim. Ganz ehrlich ist es eigentlich immer darum gegangen, die bestehende A656 zu verwenden – diese Straße ist zwar nicht besonders schön, würde aber die technischen Voraussetzungen an einen Radschnellweg durchaus erfüllen. Soweit es mich betrifft, könnten sie das Ding für Autos sperren und es als Radschnellweg deklarieren: Wäre fürs Erste ok.

In der Realität sind diese Demos natürlich nie auf einer, schauder, Bundesautobahn gefahren, jedenfalls nicht den ganzen Weg. Dieses Mal aber waren wir immerhin ein kleines Stück auf einer leibhaftigen Autobahn unterwegs, für vielleicht 500 Meter auf der A656 vor Mannheim, mit offiziellem Segen und von der begleitenden Polizei zelebriert wie ein Hochamt.

Jaja, Velorution, der Übergang von einer Auto- in eine Fahrradgesellschaft, in der der Wahnsinn aus der Dystopie des Herrn Benz durch entspannte Mobilität und selbstbestimmten Umgang mit Verkehrstechnik ersetzt würde: die sieht anders aus. Aber vielleicht hat die Standpauke[1], die eine Vertretrin des Radentscheid Heidelberg den mitfahrenden Offiziellen (ja, der Heidelberger OB und der Mannheimer „Verkehrsbürgermeister“ sind tatsächlich die ganze Strecke mitgefahren) bei der Abschlusskundgebunge gehalten hat, diese ja vielleicht doch so weit beeindruckt, dass wenigstens zwei oder drei Parkplätze im nächsten Jahr verschwinden werden. Und das wäre ja schon mal ein Gewinn.

Fahrräder auf einer autobahnähnlichen Straße, ein Anhänger mit Blumen

So sieht Velorution aus: Menschen und Blumen auf der Autobahn.

[1]

Es war großartig: Während die Bürgermeister wieder davon geredet haben, dass es nur noch ein paar „Lückenschlüsse“ brauche, beschrieb die Rednerin die Untätigkeit der Verwaltungen und die düstere Realität, in der nicht ein Parkplatz weichen darf, während die Bürgermeister im Stil gescholtener Schulbuben danebenstanden. Sehr charmant und mit viel Applaus bedacht. Wenn das dem Apparat nicht etwas mehr Realitätssinn vermittelt…

Wifi im Metronom: Ui

12022:191:9 ( 2022-07-11)

Das Captive Portal im WLAN vom Metronom, gerendert in einem netsurf: Nicht perfekt, aber es funktioniert, ganz ohne Javascript und anderen Zauber.

Ich sage ja nur ungern etwas Positives über Epiphänomene der Bahnprivatisierung, aber wo ich gerade in einem Metronom sitze und ich wiederholt über absurd komplexe Captive Portals geschimpft habe: Die Metronoms (bzw. ihr Dienstleister Icomera) machen das tatsächlich mal so, dass das halbwegs akzeptabel ist: Es funktioniert ohne Javascript und Local Storage, auch im netsurf (wenn auch interessanterweise nicht mit dillo; ich habe das nicht debuggt) und überträgt in restriktiv konfigurierten Browsern gerade mal 6 kiB für die Seite. Selbst ein webkit kommt, solange Javascript aus ist, mit rund 50 kiB raus.

Wenn das irgendwer von Icomera liest: Ziemlich großes Lob[1]! Wenn das hier jemand liest, der/die ein kommerzielles WLAN anbieten will, es aber nicht einfach ganz offen lassen will: Geht zu Icomera und sagt: „Ich will das, was die Metronoms bekommen haben“.

Full Disclosure: Ich bin an sich ein zähnefletschender Feind von „Dienstleistern“ wie Icomera, habe aber ansonsten tatsächlich nichts mit denen zu tun.

PS: Kein Licht ohne Schatten im Geschäft von IT-„Dienstleistung“: Icomera blockt leider Port 587, der inzwischen Standard fürs Maileinliefern ist. Ach, Icomera: Drängt die Leute doch bitte nicht noch mehr zu webmail (und gmail). Aber immerhin haben sie ssh offen gelassen, so dass halbwegs unproblematische Selbsthilfe möglich ist.

[1] Für ganz großes Lob müsstet etwas zurückhaltenderes CSS verwenden oder zumindest den z-index eures Dialogs über den Footer heben.

⎆
PSA: netsurf 3 does not accept cookies from localhost

12022:190:4 ( 2022-07-10)
As I have already pointed out in April, I consider simple and compact web browsers a matter of freedom (well, Freedom as in speech, actually), and although there's been a bit of talk about ladybird lately, my favourite in this category still is netsurf, which apparently to this date is lean enough to be runnable on vintage 1990 Atari TT machines. I'll freely admit I have not tried it, but the code is there.

Yesterday, however, netsurf drove me crazy for a while: I was developing a web site, making sure it works with netsurf. This website has a cookie-based persistent login feature, and that didn't work. I sent my Set-Cookie headers all right – ngrep is your friend if you want to be sure, somewhat like this:
```
sudo ngrep -i -d lo cookie port 8888
```
Ngrep also clearly showed that netsurf really did not send any Cookie headers, so the problem wasn't on the cookie header parsing side of my program, either.

But why did the cookies disappear? Cookie policy? Ha: netsurf does accept a cookie from Google, and crunching this would be the first thing any reasonable policy would do. Did I perhaps fail to properly adhere to the standards (which is another thing netsurf tends to uncover)? Hm: looking up the cookie syntax spec gave me some confidence that I was doing the right thing. Is my Max-Age ok? Sure, it is.

The answer to this riddle: netsurf does not store cookies if it cannot sort them into a hierarchy of host names, and it never can do that for host names without dots (as in localhost, for instance). Given the ill-thought-out Domain attribute one can set for cookies (see the spec linked above if you want to shudder), I even have a solid amount of sympathy for that behaviour.

But given that that is something that will probably bite a lot of people caring about freedom enough to bother with netsurf, I am still a bit surprised that my frantic querying of search engines on that matter did not bring up the slightly unconventional cookie handling of netsurf. Let us hope this post's title will change that. Again, netsurf 3 will not store cookies for not only localhost but any host name without dots in it. Which is a bit inconvenient for development, and hence despite my sympathy I am considering a bug report.

Meanwhile, I've worked around the problem by adding:
```
127.0.0.1 victor.local.de
```
to my /etc/localhost (the name really doesn't matter as long as it will never clash with an actual site you want to talk to and it contains one or more dots) and access the site I'm developing as http://victor.local.de. Presto: my cookie comes back from netsurf all right.
A Debugging Session

So, how did I figure this riddle out? The great thing about Debian and halfway compact software like netsurf is that it makes it reasonably simple to figure out such (mis-) features. Since I firmly believe that the use of debuggers is a very basic skill everyone touching a computer should have, let me give a brief introduction here.

First, you need to get the package's source. Make sure it matches the version of the program that you actually run; to do that, copy the deb line in /etc/apt/sources.list for the repository the package comes from (note that this could be the security repo if you got updates from there). In the copied line, replace deb with deb-src. In my case, that would be:
```
deb-src https://deb.debian.org/debian bullseye main
```
On a freshly installed Debian, it's likely you already have a line like this; consider commenting out the deb-src lines when not working with source code, as that will make your apt operations a bit faster.

After an apt update, I can now pull the source. To keep your file system tidy, I put all such sources into children of a given directory, perhaps /usr/src if you're old-school, or ~/src if not:
```
cd
mkdir -p src/netsurf
cd src/netsurf
apt-get source netsurf-gtk
```
I'm creating the intermediate netsurf directory because apt-get source creates four items in the directory, and in case you're actually building a package (which you could, based on this), more entries will follow; keeping all that mess outside of src helps a lot. Note that apt-get source does not need any special privileges. You really should run it as yourself.

By the way, this is the first part where monsters like webkit make this kind of thing really strenuous: libwebkit sources (which still are missing much over a full browser) pull 26 megabytes of archive expanding to a whopping 300 Megabytes of source-ish goo.

To go on, enter the directory that apt-get source created; in my case, that was netsurf-3.10. You can now look around, and something like:
```
find . -name "*.c" | xargs grep "set-cookie"
```
quickly brought me to a file called netsurf/content/urldb.c (yeah, you can use software like rgrep for „grep an entire tree“; but then the find/xargs combo is useful for many other tasks, too).

Since I still suspected a problem when netsurf parses my set-cookie header, the function urldb_parse_cookie in there caught my eye. It's not pretty that that function is such an endless beast of hand-crafted C (rather than a few lines of lex[1]), but it's relatively readable C, and they are clearly trying to accomodate some of the horrible practices out there (which is probably the reason they're not using lex), so just looking at the code cast increasing doubts on my hypothesis of some minor standards breach on my end.

In this way, idly browsing the source code went nowhere, and I decided I needed to see the thing in action. In order to not get lost in compiled machine code while doing that, one needs debug symbols, i.e., information that tells a debugger what compiled stuff resulted from what source code. Modern Debians have packages with these symbols in an extra repository; you can guess the naming scheme from the apt.sources string one has to use for bullseye:
```
deb http://debug.mirrors.debian.org/debian-debug bullseye-debug main
```
After another round of apt update, you can install the package netsurf-gtk-dbgsym (i.e., just append a -dbgsym to the name of the package that contains the program you want to debug). Once that's in, you can run the GNU debugger gdb:
```
gdb netsurf
```
which will drop you into a command line prompt (there's also a cool graphical front-end to gdb in Debian, ddd, but for little things like this I've found plain gdb to be less in my way). Oh, and be sure to do that in the directory with the extracted sources; only then can gdb show you the source lines (ok: you could configure it to find the sources elsewhere, but that's rarely worth the effort).

Given we want to see what happens in the function urldb_parse_cookie, we tell gdb to come back to us when the program enters that function, and then to start the program:
```
(gdb) break urldb_parse_cookie
Breakpoint 1 at 0x1a1c80: file content/urldb.c, line 1842.
(gdb) run
Starting program: /usr/bin/netsurf
```
With that, netsurf's UI comes up and I can go to my cookie-setting page. When I try to set the cookie, gdb indeed stops netsurf and asks me what to do next:
```
Thread 1 "netsurf" hit Breakpoint 1, urldb_parse_cookie (url=0x56bcbcb0,
    cookie=0xffffbf54) at content/urldb.c:1842
1842  {
(gdb) n
1853    assert(url && cookie && *cookie);
```
n (next) lets me execute the next source line (which I did here). Other basic commands include print (to see values), list (to see code), s (to step into functions, which n will just execute as one instruction), and cont (which resumes execution).

In this particular debugging session, everything went smoothly, except I needed to skip over a loop that was boring to watch stepping through code. This is exactly what gdb's until command is for: typing it at the end of the loop will fast forward over the loop execution and then come back once the loop is finished (at which point you can see what its net result is).

But if the URL parsing went just fine: Why doesn't netsurf send back my cookie?

Well, tracing on after the function returned eventually lead to this:
```
3889      suffix = nspsl_getpublicsuffix(dot);
(gdb)
3890      if (suffix == NULL) {
```
and a print(suffifx) confirmed: suffix for localhost is NULL. Looking at the source code (you remember the list command, and I usually keep the source open in an editor window, too) confirms that this makes netsurf return before storing the freshly parsed cookie, and a cookie not stored is a cookie not sent back to the originating site. Ha!

You do not want to contemplate how such a session would look like with a webkit browser or, worse, firefox or chromium, not to mention stuff you don't have the source …
⎆

Der Markov-Preis für die ungewöhnlichste Wortfolge

12022:189:8 ( 2022-07-09)

Ich bin kein besonderer Freund der Triggerwarnung an sich, aber hier warne ich mal: Es geht um Rassismus, schreckliche Gewalt (wenn das für euch einen Unterschied macht: obendrein gegen Kinder) und Religion. Eigentlich ist das alles viel zu ernst für einen Spaßpreis.

Aber es hilft nichts: Der Markov-Preis für die ungewöhnlichste Wortfolge[1] geht heute an den Deutschlandfunk für den Hintergrund Politik vom 2. Juli, dessen Thema der Sender wie folgt umschreibt:

Tausende indigene Kinder wurden zwischen 1870 und 1996 in Kanada von ihren Familien getrennt und in Internaten untergebracht. Oft wurden sie dort sexuell missbraucht, viele starben. Die Aufarbeitung dieses Kapitels der kanadischen Geschichte hat erst begonnen – und wird die Gesellschaft noch lange beschäftigen.

Darin heißt es bei Minute 12:00: „Die Nonnen hatten alle Lederpeitschen.“ Nennt mich naiv im Hinblick auf die Realität des Christentums, aber: jedenfalls außerhalb der engeren BDSM-Szene ist das schon ein Satz, dem eine durchschnittliche künstliche Intelligenz eine eher geringe Wahrscheinlichkeit zuordnen würde. Der Neugier halber habe ich kurz meinen Müllbrowser angeworfen (in dem darf liberal Javascript laufen), um zu sehen, was Google dazu einfällt:

Google-Suchfeld mit "Die Nonnen hatten alle" und vorgeschlagener Ergänzung "folgen"

Bei näherer Überlegung muss ich die Preisvergabe allerdings relativieren, denn wenn ich (erneut) an Edgar Allen Poes Kurzgeschichte Die Grube und das Pendel denke, erscheint die prämierte Wortfolge und auch ihre BDSM-Konnotation gar nicht mehr so abwegig.

Eine weitere Verbindung zu jüngeren Themen aus diesem Blog fand ich bei Minute 10:20. In der Übersetzung des Deutschlandfunks:

Sie kamen mit diesen Lastwagen, mit denen sonst Vieh transportiert wird. Damit haben sie uns abgeholt…

…nämlich in die besagten residential schools.

Ich glaube, es ist kein Zufall, dass da Fahrzeuge eingesetzt wurden, die normalerweise Schlachttiere bewegen. Gegen Ende meiner Überlegungen zu Königinnenkämpfen neulich hatte ich schon darauf hingewiesen, dass die Charakterisierung von Menschen als lästige (oder im vorliegenden Fall zu tötende) Tiere ein „konstantes Feature so gut wie aller Kriege und anderer Massenmorde der Geschichte“ ist.

Ganz gewiss hat es der Transport der Kinder in Schlachtvieh-Wagen den im Apparat beschäftigten Menschen erheblich leichter gemacht, so unmenschlich zu handeln. Und ja, das ist sowohl ein Argument für die Erhaltung der Empathie mit Schlachtvieh als auch ein Argument gegen den Transport von Menschen in Viehtranportern[2].

[1]

Benannt ist der Preis nach Andrei Andrejewitsch Markow in seiner in Fachkreisen üblicheren englischen Umschreibung (sich selbst wird er wohl vor allem Марков geschrieben haben). Markov-Ketten waren bis zum Durchmarsch der neuronalen Netze das Mittel der Wahl zur statistischen Modellierung sprachlicher Äußerungen, also letztlich zur Beantwortung der Frage, wie wahrscheinlich es ist, kurz nach dem Token „Nonne“ ein Token wie „Hostie“, „Backschaufel“, „Gesangbuch“, „Rohrstock“ oder eben „Lederpeitsche“ zu finden.

[2]

Auch wenn ich irgendwelche Nazigeschichten hier lieber raushalten würde (denn da ist nochmal was ganz anderes passiert), muss ich, wo ich schon grob das Thema habe, noch anmerken: Ich bin überzeugt, dass Adolf Eichmann nicht nur aus Sachzwang Viehwaggons gewählt hat, um all die Menschen in die NS-Vernichtungslager verschleppen zu lassen.

Bertrand Russell und die Faulheit

12022:185:0 ( 2022-07-04)
Als ich angefangen habe, an diesem Blog zu schreiben, wollte ich eigentlich regelmäßig über den Wahnsinn ranten, dass wir Unmengen Plunder und „Dienstleistungen“ herstellen, ohne die die Welt eigentlich besser wäre, und dafür sowohl uns selbst als auch den Planeten furchtbar stressen. Wenn ich jetzt sehe, was ich wirklich unter dem Tag Faulheit geschrieben habe: Am Schluss gab es doch immer andere Themen.

Unterdessen war am 18. Mai der 150. Geburtstag von Bertrand Russell, von dem hier verschiedentlich schon die Rede war, allerdings eher im Zusammenhang mit seiner Philosophiegeschichte und weniger aufgrund seiner Arbeiten an den Grundlagen der Mathematik, seiner zähen Arbeit gegen religiösen Wahn oder seines pazifistischen Elans[1]; mit all dem hat mich Russell schon sehr lange begeistert.

Erst im Portrait von Russell in SWR2 Wissen am 13.5. (Audio lohnt sich: Russell spricht selbst, Englisch und Deutsch!) jedoch erfuhr ich, dass er mal wegen Aufruf zu Widerstand gegen die Staatsgewalt im Gefängnis saß (zudem im Alter von 89 Jahren) – und, dass er schon 1932 die zornige Diatribe gegen den Unsinn exzessiver Lohnarbeit geschrieben hat, die ich für diesen Blog vorgesehen hatte.

Sind wir 90 Jahren später klüger?

Allerdings schrieb Russell seinen kleinen Aufsatz auf dem Höhepunkt der Großen Depression, also unter fantastischen Arbeitslosenraten, und so unterscheidet sich seine Analyse schon in vielem von meiner; der wichtigste Punkt wäre wohl, dass Russell in erster Linie die vorhandene Arbeit gleichmäßiger verteilen wollte, während ich, 90 Jahre später, überzeugt bin, dass die Gesamtmenge an Arbeit drastisch reduziert werden muss und kann, um den allgemeinen Wohlstand zu heben. Aber wir haben eben auch 90 Jahre Produktivitätssteigerung trotz Übergangs in die „Dienstleistungsgesellschaft“ hinter uns, und Russell konnte nichts von Indexfonds, Fidget Spinnern, SAP, SUVs, Nagelstudios, Bundesligafernsehen, Rechteverwertungsgesellschaften, Flimmerwände, TikTok und all dem anderen bunten Mist wissen, mit dem wir uns heute das Leben gegenseitig schwer machen.

Russells Essay „In Praise of Idleness“ ist beim Web Archive zu haben (fragt mich nicht, wie das gerade mal 50 Jahre nach Russells Tod trotz Contentmafia zugeht; schlechter auf Deutsch), und wo ich ihn schon gelesen habe, möchte ich ein paar der schöneren Zitate hier versammeln, zumal seine Argumente inzwischen vielleicht unvollständig, sicher aber nicht falsch sind. Die Übersetzungen sind jeweils von mir.

Russell fängt mit etwas an, das zwar zu lang ist, um ein gutes Gaffito zu machen, und vielleicht klingt „rechtschaffen“ („virtuous“) ein wenig angestaubt. Ich würde damit dennoch jeden Tag auf eine Fridays For Future-Demo gehen:

Ich glaube, dass viel zu viel Arbeit getan wird in der Welt, und dass der Glaube, Arbeit sei rechtschaffen, unermesslichen Schaden anrichtet [...]

Original

I think that there is far too much work done in the world, that immense harm is caused by the belief that work is virtuous [...]

Ursprüngliche Gewalt

Im Weiteren leitet Russell die „Arbeitsethik“ in etwa dadurch ab, dass früher mal Krieger die Leute, die die Arbeit gemacht haben, nicht dauernd mit Gewalt zwingen wollten, sie zu füttern. Russell, der ja Kommunist gewesen war, bis er Lenin getroffen hat, waren gewiss die Parallelen zu Marx' ursprünglicher Akkumulation[2] bewusst; ich frage mich ein wenig, warum er darauf nicht wenigstens kurz anspielt.

Und dann kommt seine scharfe Beobachtung, dass es während des ersten Weltkriegs mit all seiner völlig destruktiven Verschwendung den ArbeiterInnen im UK eigentlich besser ging als in Zeiten ganz normalen Wirtschaftens:

Trotz all [der Verschwendung aufs Töten] war das generelle Wohlstandsniveau der ungelernten LohnarbeiterInnen auf der Seite der Alliierten höher als davor oder danach. Die tatsächliche Bedeutung dieser Tatsache wurde durch Finanzpolitik versteckt: Die Kriegsanleihen ließen es so aussehen, als würde die Zukunft die Gegenwart ernähren. Aber das ist natürlich unmöglich; ein Mensch kann keinen Brotlaib essen, der noch nicht existiert.

Original

In spite of this, the general level of physical well-being among unskilled wage-earners on the side of the Allies was higher than before or since. The significance of this fact was concealed by finance: borrowing made it appear as if the future was nourishing the present. But that, of course, would have been impossible; a man cannot eat a loaf of bread that does not yet exist.

Diese Argumentation zeigt in der anderen Richtung übrigens den Unsinn (oder die Fiesheit) kapitalgedeckter Rentenversicherungen: Wenn in 50 Jahren niemand mehr Brot backt, wird es für all das angesparte und zwischenzeitlich zerstörerische Kapital kein Brot zu kaufen geben – über diesen spezifischen Wahnsinn hatte ich es schon kurz im letzten April.

In diesem speziellen Fall würde ich Russell allerdings fragen wollen, ob das ähnlich auch für die britischen Kolonien galt; einige indische Hungersnöte im Megaopferbereich fallen durchaus in die verschiedenen Kriegszeiten, und ich vermute, Russell sieht hier zu guten Stücken lediglich die während Kriegen erheblich größere Kampfkraft nicht allzu patriotischer Gewerkschaften reflektiert.

Philosophie und Sklavenhaltung

Wenig später folgt ein weiteres Bonmot, wenn Russell zunächst die immer noch herrschende Ideologie erklärt:

Warum [sollten Leute ohne Lohnarbeit verhungern und die anderen furchtbar lang arbeiten]? Weil Arbeit Pflicht ist, und Menschen nicht im Verhältnis zu dem bezahlt werden sollen, was sie herstellen, sondern im Verhältnis zu ihrer Tugendhaftigkeit, wie sie durch ihren Fleiß unter Beweis gestellt wird.

Das ist die Moralität des Sklavenstaates, angewandt auf Umstände, die völlig verschieden sind von denen, unter denen sie entstand.

Original

Why? Because work is a duty, and a man should not receive wages in proportion to what he has produced, but in proportion to his virtue as exemplified by his industry.

This is the morality of the Slave State, applied in circumstances totally unlike those in which it arose.

Ich merke kurz an, dass Russell als Philosoph dem antiken Sklavenstaat durchaus etwas abgewinnen konnte, denn ohne die Arbeit all der SklavInnen hätten Thales und Demokrit wohl keine Muße gehabt, ihren von Russell sehr geschätzten Gedanken nachzuhängen. Dabei ist er gar nicht so furchtbar darauf fixiert, dass die Leute in ihrer Muße dringend philosophieren[3] müssen:

Es wird der Einwand kommen, dass, wenn auch ein wenig Muße angenehm ist, die Leute nicht wüssten, mit was sie ihre Tage füllen sollen, wenn sie nur vier Stunden von ihren vierundzwanzig arbeiten müssen. Soweit das in unserer modernen Welt wirklich zutrifft, ist es eine Verdammung unserer Zivilisation; es war jedenfalls in keiner vorherigen Epoche wahr. Es hat vor uns eine Fähigkeit gegeben für Freude und Spiel, die in gewissem Maß von unserem aktuellen Kult der Effizienz gehemmt wird. Der moderne Mensch denkt, dass es für jede Tätigkeit einen Grund außerhalb ihrer selbst geben müsse, dass Dinge nie um ihrer selbst willen getan werden dürfen.

Original

It will be said that, while a little leisure is pleasant, men would not know how to fill their days if they had only four hours of work out of the twenty-four. In so far as this is true in the modern world, it is a condemnation of our civilization; it would not have been true at any earlier period. There was formerly a capacity for lightheartedness and play which has been to some extent inhibited by the cult of efficiency. The modern man thinks that everything ought to be done for the sake of something else, and never for its own sake.

Die lahmeren Einwände gegen das bedingungslose Grundeinkommen kamen also auch damals schon. Ich stimme Russells Entgegnug aus diesem Absatz herzlich zu, auch wenn er wie ich auch nicht widerstehen kann, kurz darauf von einer generellen Begeisterung für Wissenschaft zu träumen:

In einer Welt, in der niemand gezwungen ist, mehr als vier Stunden pro Tag zu arbeiten, wird jede Person, die die wissenschaftliche Neugier packt, sich dieser hingeben können, und alle MalerInnen werden malen können, ohne zu verhungern, gleichgültig, wie großartig ihre Bilder sein mögen.

Original

In a world where no one is compelled to work more than four hours a day, every person possessed of scientific curiosity will be able to indulge it, and every painter will be able to paint without starving, however excellent his pictures may be.

Nun… Bis zum Beweis des Gegenteils glaube ich fest daran, dass eine Gesellschaft mit minimalem Lohnarbeitszwang eine Gesellschaft von BastlerInnen und Amateurastronominnen sein wird. Schaun wir mal.

Krieg ist viel Arbeit

Ich kann dieses Best-of aus Russells Artikel nicht ohne seine Brücken zum Kriegführen beenden. Krieg erwähnt er, wenn er Techniken diskutiert, die die Übersetzung von Produktivitätsfortschritten in weniger Arbeit verhindern:

Wenn sich alle diese Methoden als unzureichend herausstellen, machen wir Krieg; wir lassen ein paar Leute Explosivstoffe herstellen und ein paar andere diese zünden, ganz als wären wir Kinder, die gerade Feuerwerk entdeckt haben.

Original

When all these methods prove inadequate, we have a war; we cause a number of people to manufacture high explosives, and a number of others to explode them, as if we were children who had just discovered fireworks.

Und dann sagt er in der Abteilung Utopie:

[Wenn die Leute nicht mehr so wahnsinnig viel arbeiten,] wird der der Hunger nach Krieg aussterben, teils aus diesem Grund [weil die Leute netter und weniger misstrauisch wären] und teils, weil Krieg viel und schwere Arbeit mit sich bringen würde.

Original

The …
⎆
Libellen aufs Kreuz gelegt

12022:183:9 ( 2022-07-03)
Diese Libelle – ausweislich der leeren Larvenhülle halbrechts unten wahrscheinlich gerade erst geschlüpft – ist hoffentlich Zeit ihres Lebens (ein paar Wochen im Sommer 2020) mit sehenden Augen in der Gegend vom Weißen Stein herumgeflogen.
Als ich in den Kurzmeldungen in Forschung aktuell vom 16.5. (ab Minute 1:50) davon hörte, wie Leute Libellen auf den Rücken gedreht und dann fallen gelassen haben, habe ich unmittelbar Lausbuben assoziiert, die strampelnden Käfern zusehen. Das hörte sich nach einer vergleichsweise eher gutgelaunten Angelegenheit für meine fiktionale Ethikkommission an. Jetzt, wo ich die zugrundeliegende Arbeit, „Recovery mechanisms in the dragonfly righting reflex“, Science 376 (2022), S. 754, doi:10.1126/science.abg0946, gelesen habe, muss ich das mit der guten Laune etwas relativieren.

Zunächst beeindruckt dabei der interdisziplinäre Ansatz. Hauptautorin ist Jane Wang, Physikerin von der Cornell University (kein Wunder also, dass im Paper eine Differentialgleichung gelöst wird), mitgeholfen haben der Luftfahrtingenieur James Melfi (auch von Cornell; kein Wunder, dass rechts und links Euler-Winkel gemessen werden) und der Neurobiologe Anthony Leonardo, der am Janelia Resarch Campus in Virgina arbeitet, augenscheinlich eine Biomed-Edeleinrichtung im Umland von Washington DC.

Zusammen haben sie mit Hochgeschwindingkeitskameras eine Variante des Schwarzweiß-Klassikers „Wie eine Katze auf den Füßen landet“[1] aufgenommen, dieses Mal eben mit Libellen. Dabei haben sie den Libellen einen Magneten auf den Bauch geklebt, sie mit diesem in Rückenlage an einem Elektromagneten festgeklemmt, gewartet, bis sich die Tiere beruhigt hatten und dann den Strom des Elektromagneten abgeschaltet, so dass die Libellen (im physikalischen Sinn) frei fielen.

Libellen rollen präzise nach rechts

Wenn das exakt so gemacht war, war offenbar sehr vorhersehbar, was die Libellen taten. Wang et al geben an, es sei ganz entscheidend, dass die Füße der Tiere in der Luft hängen, weil sonst einerseits eigene Reflexe von den Beinen ausgelöst würden und andererseits die Libellen selbst starten wollen könnten: „voluntary take-off via leg-kicks introduces a large variability“.

Bis dahin regt sich meine Empathie nur wenig. Zwar schätzen es die Libellen ganz sicher nicht, auf diese Weise festgehalten zu werden. Aber andererseits ist das alles ganz gut gemacht, und die Ergebnisse der Studie sind soweit ganz überzeugend und beeindruckend. Die Tiere drehen sich konsistent um ihre Längsachse, um wieder auf den Bauch zu kommen, fangen mit der Drehung nach gerade mal 100 ms an (als Reaktionszeit für Menschen gelten so etwa 300 ms; aber ok, wir haben auch viel längere Nerven) und sind dann nach gut zwei Zehntelsekunden oder vier Flügelschlägen fertig, also bevor unsereins überhaupt beschlossen hätte, was zu tun ist.

Für mich unerwarteterweise findet die Drehung sehr kontrolliert und offenbar vorgeplant statt. Ich lese das aus der Tatsache, dass die Winkelgeschwindigkeit der Drehung zwischen 170 Grad (fast auf dem Rücken) und vielleicht 40 Grad (schon recht gut ausgerichtet) praktisch konstant ist. Abbildung 2 B des Papers fand ich in der Hinsicht wirklich erstaunlich: nicht vergessen, das Tier bewegt derweil ja seine Flügel.

Die AutorInnen betrachten weiter die Stellung der beiden Flügelpaare im Detail, um herauszubekommen, wie genau die Libellen die präzise Drehung hinbekommen. Das ist bestimmt sehr aufregend, wenn mensch irgendwas von Flugzeugbau versteht, aber weil ich das nicht tue, hat mich das weniger begeistert. Außerdem war ich zu dem Zeitpunkt bereits etwas voreingenommen, nachdem ich erfahren hatte, dass, um die Flügelstellung mit den Analyseprogrammen, die Wang et al hatten, rekonstruieren zu können, die Libellen mit Nagellack sechs Punkte auf die Flügel gemalt bekamen.

Die Erzählung wird düsterer

Für die Libellen noch unangenehmer dürfte, so denke ich mir, das kleines Y-förmige Plastikgestell gewesen sein, das ihnen die ExperimentatorInnen auf den Thorax geklebt haben. Sie sagen, es sei nötig, um das Bezugssystem der fallenden Libelle bestimmen zu können. Und dann gibts noch den Magneten, der die Libelle vor dem Abwurf hält: alles zusammen wiegt ungefähr 25 mg, bei einer Libelle, die selbst gerade mal ein Viertelgramm wiegt. Andererseits, und das will ich gerne glauben, nehmen heranwachsende Libellen bis zu 50 mg am Tag zu (sie haben ja auch nur ein paar Wochen Zeit als Imago), so dass sie Massenänderungen dieser Art vielleicht wirklich nicht belasten.

Wie es eine Spinne hinbekommen hat, diese Libelle zu erlegen, weiß nicht nicht. Aber immerhin sind ihre Augen und Ocellen nicht zugepinselt.

Wirklich geregt hat sich mein Mitleid – unter der Maßgabe der letzten Absätze der Geschichte mit den Wespen – aber, als es um die Frage ging, woher Libellen eigentlich ihre Orientierung kennen, woher sie also wissen, ob sie gerade auf dem Rücken fliegen oder vielleicht auf der Seite.

Die Arbeitshypothese von Wang et al war offenbar, dass das im Wesentlichen der Sehsinn ist. Moment: „Der Sehsinn“? Nein: „Die Sehsinne“. Libellen haben nämlich gleich zwei davon, einerseits ihre Facettenaugen, dazu jedoch noch einfache, nicht abbildende Sensoren, die Ocellen. Ich sags ganz ehrlich: Ich habe das Paper vor allem gelesen, weil ich wissen wollte, wie sie den Libellen die Augen und Ocellen verbunden haben.

Da ich das jetzt weiß, kenne ich die Stelle, an der ich als Ethikkommission nein gesagt hätte, denn die Sinne der Tiere wurden mit einem bestimmt nicht mehr entfernbarem Pamp aus schwarzer Farbe vermischt mit UV-blockierendem Kleber zugekleistert. Die Versuchsreihe mit geblendeten Libellen haben Wang und ein lediglich in den Acknowledgements erwähnter Leif Ristroph unabhängig von der ersten durchgeführt, dramatischerweise im Courant-Institut, grob als „Angewandte Mathe“ zu klassifizieren, unangenehm nah an dem, wofür ich bezahlt werde.

„Drei kamen durch“ ist kein Rezept für gute Wissenschaft

Diese beiden haben also vierzehn Libellen in New York City gefangen und elf weitere von KollegInnen bekommen. Und jetzt (aus dem Supplementary PDF):

Beim Bemalen der Augen und Ocellen ist es wichtig, einen feinen Pinsel zu verwenden, damit keine Farbe auf den Hals oder Mund [des Tieres] tropft.

Aus dieser Sammlung von Libellen haben drei die vollständigen Experimente überlebt, zwei der Gattung Perithemis tenera, eine der Gattung Libellula lydia. Dies umfasste die Tests mit normalem Sehsinn und mit blockierten Sehsinnen. Alle waren präzise [? Original: rigorous] Flieger. Mit funktionierendem Sehsinn rollten sie nach rechts. Sie überlebten auch mindestens zwei Kältephasen im Kühlschrank, eine vor dem Ankleben des Magnets, eine weitere vor dem Bemalen der Augen.

Original

When painting the eyes and ocelli, it is important to use a fine brush tip, so that no paint spills to the neck or to the mouth.

Of this collection, three dragonflies, two amberwing (Perithemis tenera) and one lydia (Libellula lydia, synonym, Plathemis lydia), survived the complete experiments, including the tests under normal vision and with blocked vision. All were rigorous flyers. They rolled to the right under normal vision. They also survived at least two chills in the fridge, one before fixing the magnet, and another before eye painting.

Nennt mich angesichts dessen, was wir täglich 10⁸-fach mit Hühnern, Schweinen, Rindern und Schafen machen, sentimental, aber wenn ein Protokoll von 25 Tieren 22 tötet, bevor das Experiment fertig ist, ist es nicht nur roh, sondern fast sicher auch Mist. Es ist praktisch unvorstellbar, dass bei so einer Selektion nicht dramatische Auswahleffekte auftreten, die jedes Ergebnis mit Fragezeichen in 72 pt Extra Bold, blinkend und rot, versehen.

In diesem Fall war das Ergebnis übrigens, dass die Libellen ohne Ocelli etwa 30% später mit dem Drehen anfingen und anschließend nicht mehr ins Gleichgewicht kamen, bevor die Kamera voll war (ich hätte es trotzdem nett gefunden, wenn Wang wenigstens anekdotisch berichten würde, ob sie es am Schluss geschafft haben). Mit zugepinselten Facettenaugen sind die Libellen ins Gleichgewicht gekommen, wenn auch langsamer und weniger kontrolliert. Waren Ocellen und Facettenaugen blockiert, sind die Libellen häufig einfach nur runtergefallen „like leaves“.

Was aber, wenn – ja vielleicht im Einzelfall doch existierende – nichtoptische Gleichgewichtsorgane Libellen anfälliger dafür macht, die Torturen des Experiments nicht zu überleben? Was, wenn auch die überlebenden Libellen anfangs ein nichtoptisches Gleichgewichtsorgan hatten, das aber durchs Einfrieren oder eine andere überwiegend tödliche Prozedur kaputt gegangen ist?

Hätte ich das Vorhaben ethisch begutachten müssen, wäre ich vermutlich eingestiegen auf Abschnitt 2.3 der ergänzenden Materialien (wenn etwas in der Art im Antrag gewesen wäre), in dem es heißt, „Dragonflies perform mid-air righting maneuvers often during their prey-capture maneuvers”.

Also… wenn die solche Manöver auch freiwillig fliegen, wäre es dann nicht besser gewesen, sie in solchen Situationen zu filmen? Klar, das wäre dann wahrscheinlich fies den Ködern gegenüber, die mensch ziemlich sicher fest positionieren (und damit ihrerseits festkleben) müsste, damit das mit dem Hochgeschwindigkeitsfilmen klappt. Aber trotzdem: Für mich wäre das das mildere Mittel gewesen.

Außerdem hätten die Köder ja Mücken sein können.

Nachtrag (2022-07-11)

Meine Sorgen über ethisch grenzwertige bis unhaltbare Experimente mit Insekten liegen offenbar im wissenschaftlichen Trend. Am 10. Juli haben die Science Alerts einen Beitrag über die Schmerzwahrnehmung von Insekten veröffentlicht, der einige weitere beunruhigende Experimente anführt (etwa zu Phantomschmerzen bei Drosophilen). Immer mehr sieht es aber so aus, als fände bei vielen Insekten durchaus Schmerzverarbeitung statt, auch wenn diese im Detail etwas anders funktioniert als bei uns.

[1]
Das Genre „Wir drehen Tiere auf den Rücken und lassen sie fallen“ ist ausweislich des Papers beeindruckend fruchtbar. Zumindest heißt es …
⎆

« Seite 9 / 18 »

Subqueries in SPARQL, and 50 Labels per Entity

Named Subqueries and Planner Barriers

Finally: Numbers. But what do they Mean?

Getting Labels

Determining Day and Month

Uploads, Multipart, Urlencoded, Oh My!

Making the Output Friendlier: Turtle?

Making the Output Friendlier: XSLT!

Basics: RDF in a few paragraphs

CURIEs

Long URIs in RDF?

Non-speaking URIs

Tanzende und stehende Linien

Abgeleitete Kopfzahl: mit 30⋅3600 Sachen um die Sonne

Mit 10⋅3600 Sachen mit der Sonne durch die Strom

Hegers Fazit

Pfadanalyse

BIP ist wurst

Und dann die Schurken

A Debugging Session

Sind wir 90 Jahren später klüger?

Ursprüngliche Gewalt

Philosophie und Sklavenhaltung

Krieg ist viel Arbeit

Libellen rollen präzise nach rechts

Die Erzählung wird düsterer

„Drei kamen durch“ ist kein Rezept für gute Wissenschaft

Letzte Ergänzungen