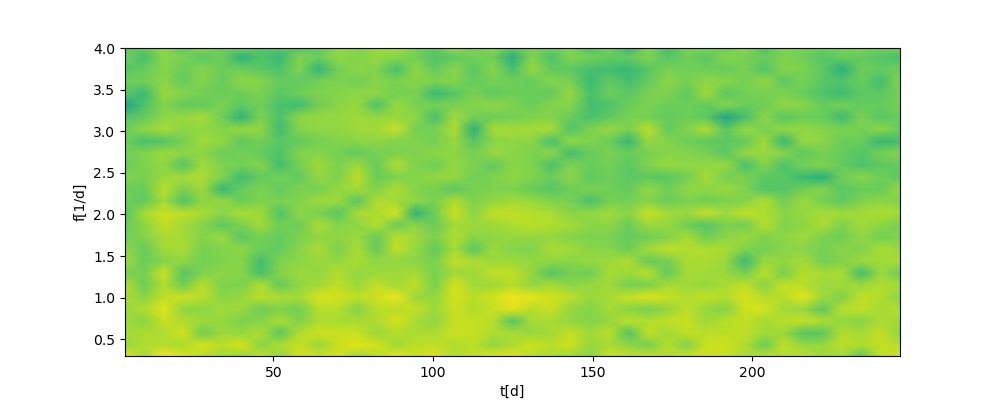
Am Ende des Posts verrate ich, welche Bewandnis es mit diesem hübschen, nachgerade frühlingshaften Muster hat. Und auch, wie mensch sowas selbst macht.
Ich habe letztes Jahr neun Monate lang CO₂-Konzentrationen auf meinem Balkon gemessen, in der Hoffnung, ein wenig hinter die Gründe für die doch überraschend großen Konzentrationsschwankungen zu kommen, für die ich bei einer ersten Messung im November 2021 nur sehr spekulative Erklärungen gefunden habe (Stand Februar vor allem: die lokale Heizung und eventuell das Kraftwerk in Rheinau oder die Chemiefabriken in Ladenburg oder Ludwigshafen). Ich habe dann neulich an der Kalibration der Daten gespielt und bin zum Schluss gekommen, dass sie nach Maßstäben von KonsumentInnenelektronik recht ordentlich sein dürften.
Jetzt möchte ich ein wenig in den Daten rumfummeln. „Explorative Datenanalyse“ nennen das Leute, die das mit dem Fummeln nicht zugeben wollen, und in der ernsthaften Wissenschaft wird zurecht etwas die Nase gerümpft, wenn jemand sowas macht: Es stecken in jedem hinreichend großen Datensatz fast beliebig viele Korrelationen, und wer sie sucht, wird sie auch finden. Leider sind (fast) alle davon Eigenschaften des Datensatzes bzw. der Messung, nicht aber des untersuchten Gegenstands.
Andererseits: Ohne Induktion (was in normale Sprache übersetzt „Rumspielen, bis mensch einen Einfall hat“ heißt) gibt es, da muss ich Karl Popper ganz heftig widersprechen, keine Erkenntnis, und Deduktion kann mensch nachher immer noch machen (also, ich jetzt nicht, weil das hier mein Freizeitvergnügen ist und keine Wissenschaft).
Erstmal glätten
Meine ganz große Enttäuschung mit dem Datensatz war ja, dass sich fast kein Jahreszeiteneffekt gezeigt hat; natürlich werde ich hier, mitten im dichtbesiedelten Oberrheingraben, kein so hübsches Signal bekommen wie die Leute mit der klassischen Messung am Mauna Loa – davon, dass ich eine Schwingung von ein paar ppm nachvollziehen könnte, ganz zu schweigen. Aber ich hatte im September 2021 unter 300 ppm gemessen, während es im Herbst auf die global eher aktuellen 400 bis 500 ppm hochging. Ich hatte gehofft, den Weg zurück zu den 300 ppm im Laufe des Sommers beobachten zu können. Doch leider ist in den (Roh-) Daten erstmal nur Gekrakel:

Wenn in einem Datensatz nur Gekrakel ist, es aber einen langfristigen Effekt geben soll, hilft oft Glätten. Dabei ersetzt mensch jeden Punkt durch einen geeignet gebildeten Mittelwert über eine größere Umgebung dieses Punktes, wodurch kurzfristiges Gewackel wie in meinen Rohdaten stark unterdrückt wird und die langfristigen Trends besser sichtbar werden sollte. Es gibt noch einen zweiten Gewinn: Mensch kann das so gewonnene Mittel von den Daten abziehen und hat sozusagen destilliertes Gewackel (den „hochfrequenten Anteil“), der auf diese Weise auch ein klareres Signal zeigen mag.
Im einfachsten Fall lässt sich so eine Glättung in ein paar Zeilen Python schreiben, und das auch noch relativ effizient als gleitendes Mittel unter Verwendung einer zweiendigen Queue aus Pythons großartigem Collections-Modul: Um das Mittel zu berechnen, addiere ich auf einen Akkumulator, und das, was ich da addiere, muss ich wieder abziehen, wenn der entsprechende Wert aus dem Fenster rausläuft. Dazu gibts noch die Subtilität, dass ich Zeit und Konzentration in der Mitte des Fensters zurückgeben will. Das führt auf so eine Funktion:
def iter_naively_smoothed(in_file, smooth_over):
queue = collections.deque()
accum = 0
for time, co2 in iter_co2(in_file):
queue.append((time, co2))
accum += co2
while time-queue[0][0]>smooth_over:
_, old = queue.popleft()
accum -= old
time, base_co2 = queue[len(queue)//2]
yield time, accum/len(queue), base_co2-accum/len(queue)
Als Plot sehen die über drei Tage[1] geglättete Konzentrationskurve und die Residuen so aus:
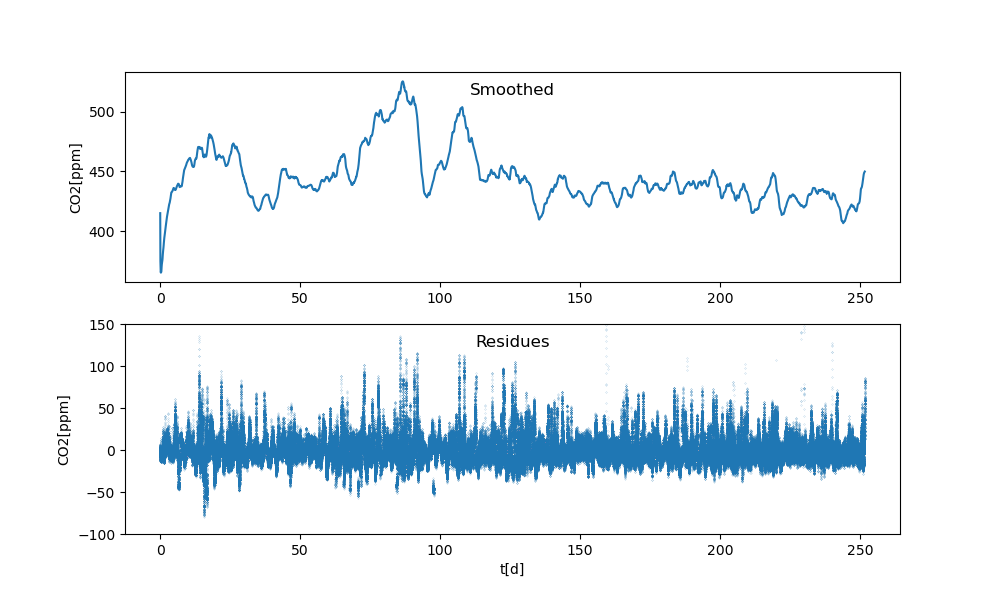
Die Ränder, vor allem der linke, sind dabei mit Vorsicht zu genießen, da dort fast nichts geglättet ist; die Funktion ist so geschrieben, dass dort die Fenster klein sind. So oder so: auch die geglättete Kurve hat keine nennenswerte Tendenz. Allenfalls die beiden großen Ausschläge bei den Tagen 80 und 110 könnten ein Signal sein.
Zeitrechnungen
„Tag 80” ist jetzt keine wirklich intuitive Angabe, aber ich wollte in den Plots nicht mit läsitgen Kalenderdaten operieren. Für die Interpretation wären sie jedoch schon ganz gut. Wie komme ich von Messtag auf ein bürgerliches Datum?
Die Daten kommen original mit Unix-Timestamps, also der Zahl der Sekunden seit dem 1.1.1970, 0:00 Uhr UTC, und sie fangen mit 1640612194 an. Um ausgehend davon bürgerliche Daten auszurechnen, muss mensch wissen, dass ein Tag 86400 Sekunden hat. Pythons datetime-Modul liefert dann:
>>> import datetime >>> datetime.datetime.fromtimestamp(1640612194+80*86400) datetime.datetime(2022, 3, 17, 14, 36, 34) >>> datetime.datetime.fromtimestamp(1640612194+110*86400) datetime.datetime(2022, 4, 16, 15, 36, 34)
Mitte März und Mitte April ist also möglicherweise was Interessantes passiert. Da gucke ich nochmal drauf, wenn ich demnächst Wetterdaten einbeziehe.
Die andere Seite, die Residuen, kann ich für eine saubere Fassung des Tagesplots aus Teil 1 verwenden. Weil längerfristige Schwankungen bei ihnen rausgerechnet sind, sollte ein regelmäßiger Tagesgang in den Residuen deutlicher herauskommen als im ganzen Signal. Dazu nehme ich wieder den Rest bei der Division durch 86400 (siehe oben), und die Warnungen wegen Zeitzonen aus dem Kalibrationspost gelten immer noch.
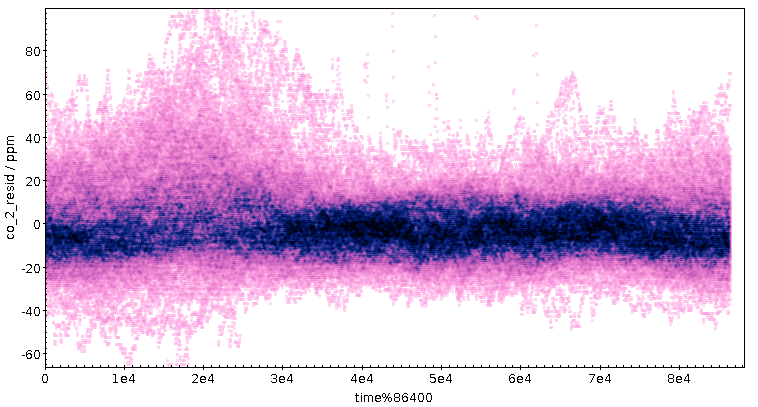
Dass da „am Morgen” (15000 Sekunden sind etwa 4:15 Uhr UTC, also 5:15 MEZ und 6:15 MESZ) irgendwas passiert, dürfte ein robustes Signal sein, und es kommt ohne die niederfrequenten Signale deutlich besser raus. Mit etwas Wohlwollen könnte mensch vielleicht sogar zwei Berge im Abstand von einer Stunde sehen, was dann Normal- und Sommerzeit entspräche. Da der Sensor nicht weit von der Bundesstraße 3 stand, liegt als Erklärung zunächst Berufs- und Pendelverkehr nahe.
Wenn der Tagesgang tatsächlich mit dem Berufsverkehr am Morgen zu tun hat, müsste sich eigentlich ein Signal im Wochenrhythmus zeigen, denn zumindest Sonntags ist es hier am Morgen deutlich ruhiger als an Werktagen. Die Projektion auf die Woche ist einfach: Statt den Rest bei der Division durch 86'400 nehme ich jetzt den Rest bei der Division durch 604'800, die Zahl der Sekunden in einer Woche. Das Ergebnis zeigt, vielleicht etwas überraschend, das Tagessignal eher deutlicher; ein Wochensignal hingegen ist weniger überzeugend erkennbar:
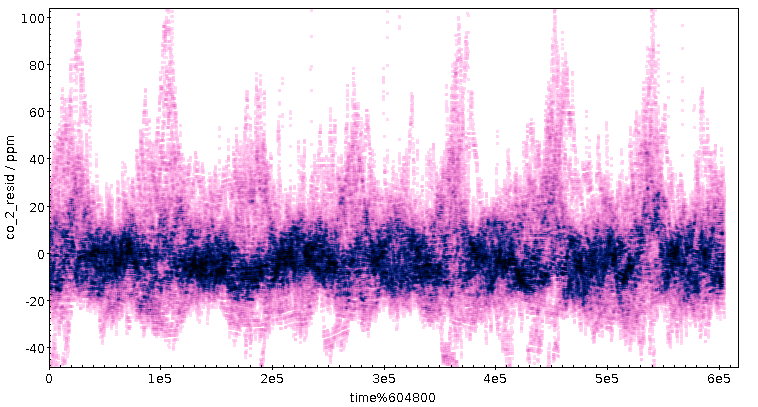
Vielleicht ist an den Tagen drei und vier etwas weniger los – welche Wochentage sind das? Nun, ich dividiere hier Unix-Timestamps; ihr erinnert euch: Die Sekunden seit dem 1.1.1970. Welcher Wochentag war dieser 1.1.?
$ cal 1 1970
January 1970
Su Mo Tu We Th Fr Sa
1 2 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30 31
Weil die Unix-Epoche so eine große Rolle im heutigen Leben spielt[2], nehme das mal als erweiterte Kopfzahl: Er war ein Donnerstag. Und so sind die Tage 3 und 4 tatsächlich Samstag und Sonntag. Meine Autoabgas-These ist mir durch diese Prüfung etwas sympathischer geworden. Vermutlich fallen die Abgase nur bei wenig Wind und wenig Thermik (das ist praktisch die berüchtigte Dunkelflaute…) auf, so dass das dunkle Band mit hoher Punktdichte mehr oder minder bei der Null bleibt, jedoch immer wieder Spitzen mit bis zu 100 ppm extra in der Rush Hour auftreten. Wenn das hier Wissenschaft wäre, müsste ich mich jetzt auf die Suche nach Daten aus der Verkehrszählung machen.
Und ich müsste überlegen, ob die Zacken im dunklen Band nicht doch ein echtes Signal sind. Speziell der Durchhänger so um die 180'000 Sekunden (also in der Nacht von Freitag auf Samstag) ist eigentlich kaum wegzudiskutieren. Aber was könnte gerade da plausiblerweise mehr frische Luft heranführen? Oder ist das, weil die Freitagnacht wegen Spätcorona noch besonders ruhig war?
In Sachen Spitzen am Morgen hätte ich eine Alternativhypothese zu den Autoabgasen: Das könnte nämlich wieder der lokale Brenner sein. Dann wäre das, was da zu sehen ist, die Warmwasserbereitung zur Morgendusche. Attraktiv ist diese These schon allein, weil mir 6:15 eigentlich ein wenig früh vorkommt für das Einsetzen der Rush Hour nach Heidelberg rein; es ist ja nicht so, als seien da noch viele nennenswerte Industriebetriebe, in denen die Leute um sieben stechen müssten. Allerdings: in einem Wohnblock mit so vielen Studis wie meinem hier ist 6:15 auch keine plausible Zeit für massenhaftes Duschen…
Spektralanalyse
Was ich gerade gemacht habe, ist ein Spezialfall einer gerade für uns AstrophysikerInnen extrem wichtigen Technik – ich habe nämlich ein Signal nach Frequenzen aufgeteilt. Bis hierher hatte ich nur in zwei Bänder, ein hohes und ein tiefes. Mit der Fourieranalyse geht das viel allgemeiner: Mensch steckt ein Signal rein und bekommt ein Spektrum heraus, eine Kurve, die für jede Frequenz sagt, wie stark Schwingungen auf dieser Frequenz zum Signal beitragen.
Mit dem Universal-Werkzeugkasten scipy kriegt mensch so ein Spektrum in anderthalb Zeilen Python:
from scipy import signal f, power = signal.periodogram(samples[:,1], fs=86400/24/120)
Dabei übergebe ich nur meine Konzentrationsmessungen, nicht die zugehörigen Zeiten, weil die periodogram-Funktion nur mit gleichmäßig gesampleten Daten zurechtkommt. Das sind meine Daten zum Glück: zwischen zwei Messungen liegen immer 30 Sekunden, und es sind auch keine Lücken in den Daten.
Die halbe Minute Abstand zwischen zwei Punkten übergebe ich im Argument fs, allerdings als Frequenz (der Kehrwert der Periode) und umgerechnet in die Einheit „pro Tag“ (schon wieder die 86400). Für einen SI-Fanatiker wie mich ist 1/d schon eine kleine Überwindung, aber für alles, was mit Pflanzen und Tieren (bzw. ihren Maschinen) in mittleren Breiten zu tun hat, ist der Tag einfach eine zu natürliche Einheit, um sie nicht zu verwenden. Am Fuß des Posts ist übrigens ein Link auf den gesamten Code, wo ihr das im Kontext sehen könnt.
Das Ergebnis sieht für meine geglättete Kurve und die Residuen so aus:
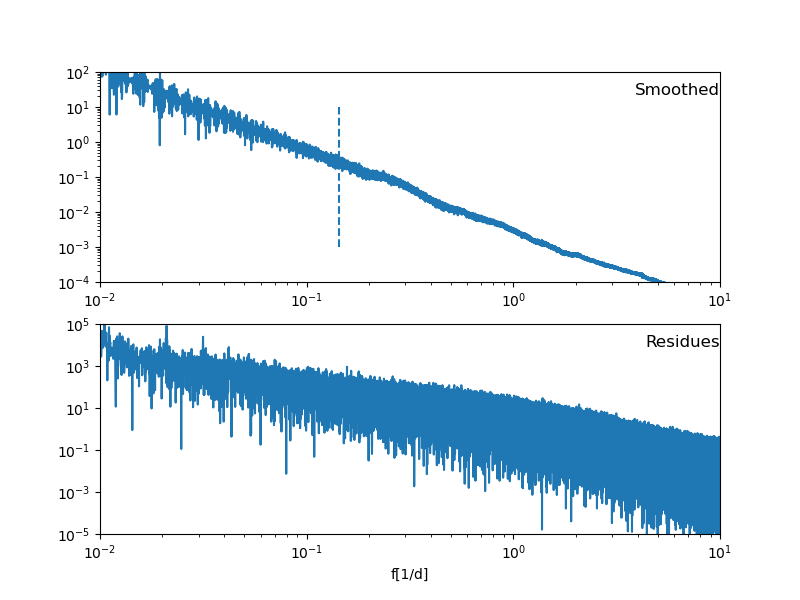
Die obere Kurve ist zumindest insofern befriedigend, als sich bei hohen Frequenzen (also: hier schwingt was mehrmals am Tag; 101 heißt hier „zehn Mal am Tag“) wenig tut. Klar: das haben wir ja rausgefiltert. Umgekehrt hätten wir bei den Residuen gerne, dass die niedrigen Frequenzen unterdrückt sind, was hier so gar nicht der Fall ist. Dazu komme ich gleich.
Wir haben oben eine gewisse Wochenperiodizität festgestellt; ich hätte also gehofft, dass sich bei einer Frequenz von 1/7 etwas im Spektrum des geglätteten Signals zeigt; ich habe die Stelle im Graph mit einer gestrichelten Linie markiert und sehe da so auf den ersten Blick gar nichts. Der kleine Buckel rechts davon könnte Physik enthalten; aber die zugehörige Periode ist beunruhigend nah an den drei Tagen, über die ich mein Fenster erstrecken lasse.
Ein paar Worte zur Fourieranalyse
Und in der Tat lässt das regelmäßige Gewackel links im Smoothed-Teil schon Böses ahnen. Das naive Glätten, dessen Code ich oben gegeben habe, hat nämlich Schwächen – die für viele Anwendungen wurst sind, die mensch aber im Kopf haben muss. Hier erstmal noch das Problem in groß:
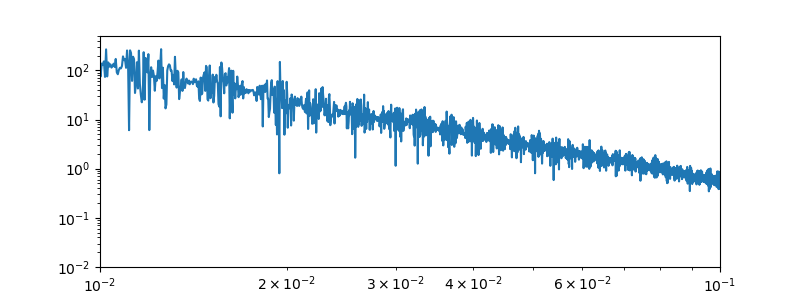
Wir sind hier im Bereich von Schwingungsperioden zwischen 10 und 100 Tagen, und da zeigt sich eine verdammt gleichmäßige Struktur von Knoten und Bäuchen; bei solchen Bildern liegt immer der Gedanke an Interferenz und Schwebung nahe. Aber was würde hier interferieren?
Dazu braucht es ein Exkurs in die Mathematik: Was ich hier beim Glätten mache, heißt dort Faltung: Mensch nudelt eine Funktion durch eine andere durch. Hier ist die eine Funktion meine CO₂-Kurve, die andere ein Kasten mit der Breite von drei Tagen und scharfen Kanten. Das „Nudeln“ von oben heißt etwas konkreter, dass ich die Faltung an der Stelle x ausrechne, indem ich meinen Kasten dorthin schaffe, ihn auf die CO₂-Kurve draufmultipliziere und das, was rauskommt, zusammenaddiere. Die Wikipedia erklärt das (ahem) verständlicher, aber „eine Funktion durch eine andere durchnudeln“ ist vielleicht eine für diese Betrachtung hinreichende Vorstellung.
Die Faltung hat nun eine fast magische Verbindung zur Fourieranalyse (also dem Ding hinter signal.periodogram): Wenn du die beiden Funktionen in einer Faltung fouriertransformierst, die Transformierten zusammenmultiplizierst und das Ergebnis zurücktransformierst, ist das Ergebnis genau die Faltung, also das Durchnudeln wie oben im Code. „Die Faltung wird im Fourierraum zu einer Multiplikation“ ist eine Aussage, mit der ihr unter MathematikerInnen ersten AdeptInnenstatus gewinnen könnt. Ich jedenfalls finde das immer wieder großartig.
Auch hier hilft Herr Gauß
Was bedeutet das hier? Nun, unsere Fensterfunktion, das platte Rechteck, hat ein richtig breites Spektrum (vgl. Rechteckfunktion in der Wikipedia – oder schreibt euch selbst ein paar Zeilen Python um signal.periodogram herum, um das Spektrum anzusehen). Unsere einfache Python-Funktion oben bringt dieses breite Spektrum in das von ihr geglättete Signal. Das zauberhafte Muster im niederfrequenten Bereich des Spektrums nach dem Glätten kommt wirklich aus den paar Zeilen Python von oben mit ein paar simplen Additionen und Divisionen. Ich finde das wirklich ein Wunder der Mathematik.
Um das besser zu machen, bietet sich zum glättenden Falten eine Funktion an, die ein weniger breites Spektrum hat als der Rechteckpuls. Das Schweizer Taschenmesser der Naturwissenschaften, die Gaußkurve, ist auch hier nützlich, denn ihre Fouriertransformierte ist, noch ein Wunder der Mathematik, wieder eine Gaußkurve. Wow.
Mit ihr zu glätten braucht, wenn es halbweg effizient sein soll, etwas mehr Aufwand als die paar Zeilen Python für die Rechteck-Glättung. Scipy erledigt das aber relativ entspannt:
window = signal.windows.gaussian(window_width, window_width/5) window /= sum(window) smoothed = signal.convolve(samples, window, "same")
(„convolve“ ist Englisch für „falten” im mathematischen Sinn). Die Division durch sum(window) „normiert die Fensterfunktion“ darauf, dass ihre Summe selbst Eins ist. Das wiederum sorgt dafür, dass beim Multiplizieren und Zusammenaddieren sich im Mittel an den CO₂-Werten nichts ändert.
Wenn ich wieder so glätte, dass ein paar Tage zusammengefasst werden, ist das Ergebnis fürs Auge nicht viel anders als bei der Glättung mit der Rechteckfunktion (hier sind durchgezogen die geglätteten Daten, während die Punktwolke die ursprüngliche Funktion darstellt):
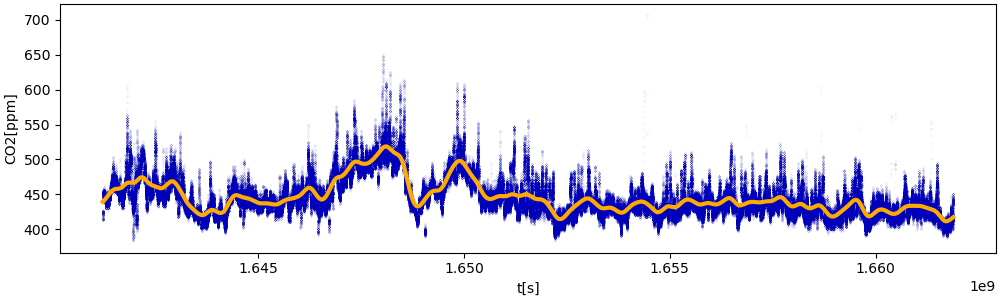
Die Spektren sehen aber ganz anders aus, und zwar viel mehr so, wie es bei einem Hoch- beziehungsweise Tiefpass sein sollte:
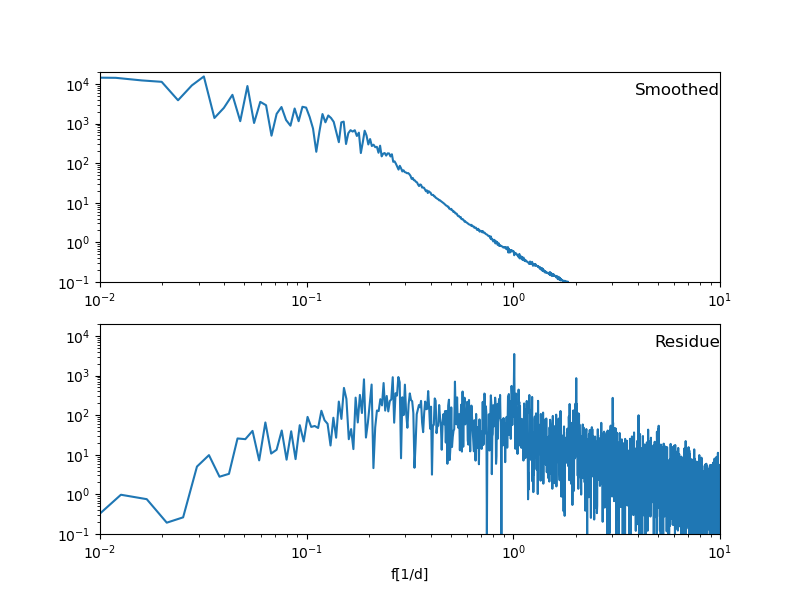
Schön ist, dass im Hochpass-Spektrum (also bei den Residuen) eine klare Spitze bei 100 (also 1) ist: Das ist der Gipfel, der häufig jeweils am Morgen auftritt, also mit einer (wenn auch nicht wirklich zuverlässigen) 24-Stunden-Periode. Weitere Spitzen sind sichtbar bei 1, 2, 3, 4 Schwingungen pro Tag, was ziemlich sicher ausschließlich daran liegt, dass der Tagesverlauf nicht einfach nur eine schöne Sinusschwingung ist (das wäre dann eine scharfe Linie bei Eins), sondern eher so ein einzelner Berg am Morgen. Diese Spitzen sind sozusagen Verwandte der Obertöne im Klang von Musikinstrumenten.
Viel was anderes, mit dem ich Hausieren gehen könnte, sehe ich allerdings aus der Grafik auch nicht.
Schließlich: Mein Spektrogramm
Schließlich kam mir noch der Gedanke, dass ja vielleicht manchmal der Tagesverlauf stärker ausgeprägt ist als sonst – etwa bei Kälte oder einer windarmen Wetterlage. Um sowas zu sehen, habe ich zur Scipy-Funktion signal.spectrogram gegriffen. Die teilt, grob gesprochen, die lange Kurve in Segmente auf und nimmt in jedem Segment so ein Spektrum. Das kann mensch dann in einer Art Heatmap plotten. Für meinen Datensatz sieht das so aus (damit über die relativ große Spanne von spektralen Intensitäten etwas zu sehen ist, plotte ich auf der Farbachse den Logarithmus):

Auch das liefert jedenfalls fürs laienhafte Auge kaum neue Ansätze. Die Vermutung, dass das Tagessignal nur dann und wann stark ist, bestätigt sich (die gelben Flecken bei der Eins sind immer wieder unterbrochen), und auch, dass die Intensitäten bei 2 und 3 (im Bild als waagrechte gelbe Flecken zu sehen) im Wesentlichen denen bei Eins folgen; es sind also wirklich eher so Obertöne des Morgenmiefs.
Zu ein paar Zeiten tut sich übers gesamte hier betrachtete Spektrum besonders wenig in der CO₂-Konzentration (etwa kurz nach Tag 50 oder kurz vor Tag 150; die senkrechten grünen Regionen), zu anderen, sichtbar durch gelbe Säulen, gibt es jede Menge Schwingungen mit jeder Menge Frequenzen (mit anderen Worten: Rauschen) im Signal, besonders rund um die Tage 15 und 110). Es würde sich wahrscheinlich lohnen, die Wetterbedingungen an diesen Tagen genau anzusehen.
Aber ansonsten: Wirklich bemerkenswerte Spuren, zu deren Verfolgung ich mich besonders dringend aufgerufen fühle, sehe ich immer noch nicht. Mal sehen, ob das bei Einbeziehung der Wetterdaten (vgl. irgendwann in der Zukunft) besser wird.
Wer mag, kann noch mitten aus der Hexenküche den Code ansehen, mit dem ich die Plots gemacht habe. Nicht alles darin ist nur Nachahmung empfohlen.
| [1] | Woher die drei Tage kommen? Nun, erstens soll die Kurve etwas glatter werden, und zweitens glaube ich ja, dass viel von dem Gewackel abseits der scharfen Spitzen von den lokalen Strömungsverhältnissen verursacht wird. Das hiesige Wetter ändert sich aber, von wenigen exotischen Wetterlagen abgesehen, ganz typisch auf Zeitskalen von drei Tagen. |
| [2] | Ich erinnere nur an das Jahr-2038-Problem, das so gegen vier Uhr unserer Zeit am Morgen am 19.1.2038… nun, ich mache mal keine Vorhersagen, wie schlimm das werden wird. |
Kommentar 1 am 2023-01-28
Zur Morgendusche Deiner Studi-Nachbarn: Die Warmwasservorbereiitung heißt ja nicht, dass das Warmwasser auch genutzt wird. Insofern ist das ja durchaus plausibel: vermutlich fängt euer Brenner irgendwann so gegen 5:30 an, auf Betriebtemperatur zu heizen und ist dann gegen 6:15 damit fertig, was einerseits in der Sommerzeit in einer Verschiebung des Peaks, anderseits aber auch in den kleinen Zeitschwankungen des Peaks zu sehen wäre, denn wann der Brenner aussetzt, hängt ja von der Temperatur im Vorhaltebehälter ab.
Vielleicht ist das ja eine Idee: der Zeitpunkt des Brennerstarts fluktuiert zeitlich nicht (anders als eventuell der Stau vor deinem Fenster). Vielleicht kommt das ja in einem Plot der Steigungen heraus? Denn das Maximum der ersten Ableitung der Wertefunktion wäre ja näher am Brennerstartzeitpunkt als das Maximum der Werte, und wäre wohl zeitlich auch zuverlässiger als die Verkehrsdichte an der Bergstraße.
Andererseits sind die Steigerungen wiederum relativ gering und jeder Furz wäre ein stärkeres Signal.
Kommentar 2 am 2023-01-29
Hmja, eine automatische Brennersteuerung, die schon mal vorsorglich anläuft, ist eine ganz plausible Geschichte. Mir ist nur beim Duschen am nächsten Tag aufgefallen, dass der ganze Gedanke einen großen Schwachpunkt hat: Zumindest hier im Haus nämlich ist die Warmwasserbereitung elektrisch. Ob der große Brenner Wohnungen, die ihm näher liegen, mit Warmwasser versorgt, weiß ich nicht. Wenn nicht, würde der Brenner im Sommer gar nicht laufen und die ganze Spur ist klar falsch. Hm. Ich denke, ich muss mal mit dem Hausmeister reden.
Und nee, wenn ich nicht muss, fange ich nicht mit dem Differenzsignal – also der diskreten Ableitung – an. Wie du richtig sagst, ist das numerisch furchtbar instabil, und bei einem ohnehin schon sehr rauschigen Signal müsste mensch da sehr sorgfältig beigehen. Das wäre echte Arbeit.
Zitiert in: „Seit bald acht Jahrzehnten nicht mehr“? „Seit bald acht Jahrzehnten nicht mehr“?
![[RSS]](./theme/image/rss.png)